A energia potencial entre dois átomos em uma molécula diatômica é dada por , onde é a distância entre os átomos e e são constantes positivas. a) Determine a força que um átomo exerce sobre o outro em função de . Faça dois gráficos, um para em função de e outro para em função de . b) Determine a distância entre os átomos para que haja equilíbrio. Esse equilíbrio é estável? c) Suponha que a distância entre os átomos seja igual à distância de equilíbrio encontrada no item (b). Qual é a energia mínima que deve ser fornecida para produzir dissociação da molécula, isto é, para separar os átomos até uma distância infinita? Esse valor denomina-se energia de dissociação da molécula. d) Para a molécula de CO, a distância de equilíbrio entre o átomo de carbono e o átomo de oxigênio é igual a e a energia de dissociação é igual a J por molécula. Calcule os valores das constantes e .
Passo 1
- Oi, galerinha! Tudo bom? Em uma molécula diatômica, temos dois átomos ligados. A energia potencial entre eles vai depender da distancia entre os dois núcleos e a carga deles. O problema forneceu a equação que descreve essa energia,
E agora queremos a partir de . Vamos lembrar que,
Derivando em relação de teremos que
Logo,
Desta forma temos que graficamente, tanto quando podem ser representados por:
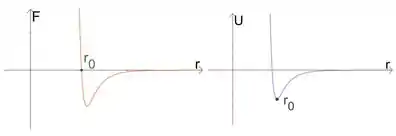
Passo 2
b) Para que haja equilíbrio, temos que a soma das forças que atuam sobre cada átomos seja zero. Como a força que cada um dos átomos sente é devida a presença do outro, apenas vamos trabalhar com as forças que atuam sobre apenas um deles. Desta forma temos que
Logo a solução de equilíbrio será
Vamos ver que tipo de equilíbrio é esse. O ponto que zera é o ponto mínimo o máximo de , já que é derivada de . A gente marcou esse ponto no gráfico de como .
Pelo gráfico, esse é um ponto de mínimo de . Por isso, esse vai ser um equilíbrio estável. Assim, é o ponto onde temos menos energia.
Passo 3
c) Queremos a variação de energia para sair de e chegar até . Em
Temos
Já para o outro caso:
Então temos que
Passo 4
Ele deu os valores para essas grandezas que acabamos de achar. Temos a distância de equilíbrio
Daí, jogando essa raiz para o outro lado
Invertendo os dois lados e multiplicando os dois lados por
Ele deu também a energia de dissociação
Ficamos com um sisteminha para resolver.
Então temos que
Depois podemos usar
Resposta
a)
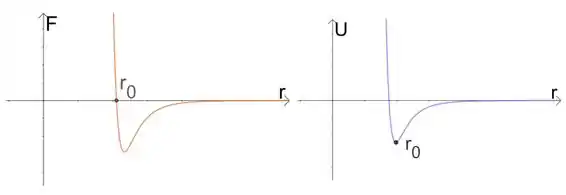
b)
c)
d) e