Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 78

Uma haste comprida e delgada, de massa M e comprimento L, está em pé sobre uma mesa. Sua extremidade inferior gira sobre um pivô livre de atrito. Um empurrão muito fraco faz a haste tombar. Ao colidir com a mesa, quanto vale (a) a velocidade angular e (b) a velocidade da extremidade superior da haste?

Passo 1

A haste longa e fina é um corpo rígido que gira em torno de um pivô sem atrito na extremidade da haste.

O torque gravitacional na haste faz com que ela gire, transformando a energia potencial gravitacional do centro de massa da haste em energia cinética rotacional.

Vamos visualizar:

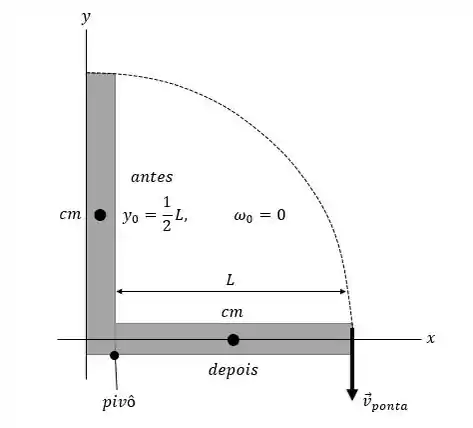
Colocamos a origem do sistema de coordenadas no ponto de articulação. Na posição inicial, o centro de massa está a uma distância de 1 2 acima da origem. Na posição final, o centro de massa está em y   =   0 me, portanto, tem energia potencial gravitacional zero.

Passo 2

  1. A equação de conservação de energia para a haste K f + U g f = K i + U g i é:

    2. 1 2 I ω 1 2 + m g y 1 = 1 2 ω 0 2 + m g y 0

    1 2 1 3 m L 2 ω 1 2 + 0   J = 0   J + m g   l 2

    ⇒ ω 1 = 3 g L

    Passo 3

  2. A velocidade na ponta da haste é

v p o n t a = ω 1 L = 3 g L .

Resposta

  1. 3 g L
  2. 3 g L .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco uniforme de raio R é cortado ao meio, de modo que uma das metades possui massa M (Figura 9.31a). a) Qual é o momento de inércia dessa metade em relação a um eixo perpendicular ao seu plano e
Um disco composto de diâmetro externo de 140,0c m é constituído de um disco maciço uniforme com raio de 50,0c m e densidade de área de 3,0g / c m 2 , cercado por um anel concêntrico com raio interno d
Uma hélice de avião possui massa de 117k g e comprimento igual a 2,08m (de uma extremidade à outra). A hélice está girando a 2400r e v / m i n em relação a um eixo que passa pelo seu centro. a) Qual é
Um balde com massa m é preso a um cabo sem massa que envolve a borda externa de uma polia uniforme e sem atrito, com raio R , semelhante ao sistema indicado na Figura 9.32 . Em termos das variáveis en
Uma corda uniforme de 3,0k g e 24,0m de comprimento está em repouso sobre o solo no topo de um rochedo vertical. Um escalador no topo deixa cair metade dela, para ajudar o amigo a escalar o rochedo. Q