Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 5
Uma bobina supercondutora tem indutância de , resistência elétrica nula e área de seção reta de . Uma fonte de corrente variável aplica à bobina uma corrente cuja variação no tempo é vista na Figura 23.13. Faça gráficos (a) da variação do campo magnético com o tempo; (b) da variação no tempo da voltagem aplicada aos terminais da bobina.
Passo 1
Fala pessoal, beleza?
Esse é um exercício um pouco mais qualitativo. Nós faremos algumas contas, mas a ideia principal dele é investigar o comportamento qualitativo das grandezas consideradas.
Na situação descrita no enunciado temos uma bobina com indutância e área atravessada por um campo magnético variável com o tempo. Com isso aparece uma corrente induzida nela, dada pelo gráfico da figura 23.13.
No item (a) queremos encontrar o perfil da variação do campo magnético com o tempo. Para isso, usamos a definição de indutância a partir do fluxo magnético:
Além disso, o fluxo será o produto do campo magnético pela área, de modo que
Com isso, o perfil do campo será o mesmo da corrente, a menos de uma escala
O gráfico da evolução temporal de será proporcional ao da corrente:
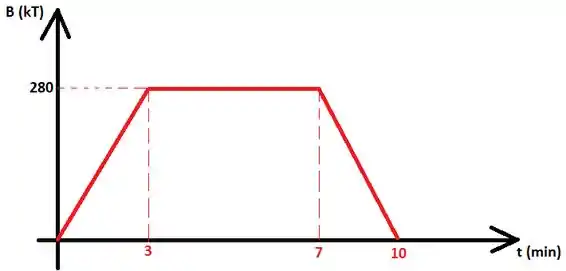
Passo 2
Já no item (b) nós queremos entender como a tensão nos terminais da bobina varia com o tempo. Para isso, recorremos a expressão
Na região , a corrente é constante, de modo que
Já nas outras regiões ela varia linearmente, de modo que a derivada temporal deve ser constante. Para , temos
Analogamente, para , segue que
Com isso, a tensão será
O gráfico será
Resposta
Esboço de gráfico.