Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 30.1 - Ex. 52
Mostre que sai de (Equacdo 30-6d e onde I=0)integrando ao longo de uma curva conveniente Cesobre uma superficie conve-
niente S de maneira semelhante a deducao da Equacao 30-9.
Passo 1
Eai galera, vamos escolher a curva com os lados e no plano xy mostrado no diagrama e aplicar a Equação 30-6d para mostrar que:
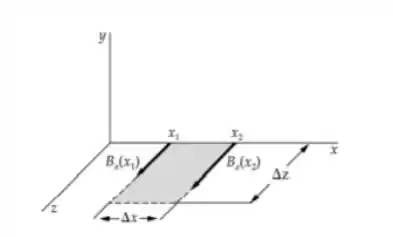
Passo 2
Como é muito pequeno, podemos aproximar a diferença em B; nos pontos por:
Então:
Ou
Resposta
Ver resolução.
Exercícios de Livros Relacionados
Um capacitor de placas quadradas de lado L está sendo descarregado por uma corrente de 0,75 A. A figura 32-28 é uma vista frontal de uma das placas, do ponto de vista do interior do capacitor. A linha
O campo magnético induzido a 6,0m m do eixo central de um capacitor de placas circulares e paralelas é 2,0 × 10 - 7T . AS placas têm 3,0m m de raio. Qual é a taxa de variação d E → / d t do campo elét
8 - O campo elétrico de uma onda eletromagnética senoidal obedece à equação E=–( 375V / m )s e n [ ( 5,97 ⋅10 15r a d / s ) t+( 1,99 ⋅ 10 7r a d / m ) x ] . Quais são a frequência, o comprimento de on
10 - Uma onda eletromagnética possui um campo magnético dado por B → ( x ,t )=( 8,25 × 10 - 9T )j ^s e n[ ( 1,38 ×10 4r a d / m ) x+ ω t ] .Em que direção e sentido a onda eletromagnética está se prop
7 - Uma onda eletromagnética senoidal com frequência igual a 6 , 10 ×10 14H z se desloca no vácuo no sentido + z . O campo magnético B é paralelo ao eixo O y e possui amplitude de 5,80 ×10 - 4 T . Esc