|| Uma bola de e outra, de , são ligadas por uma haste rígida e de massa desprezível com de comprimento. A haste gira em sentido horário em torno de seu centro de massa a . Que valor de torque a levará ao repouso em ?
Passo 1
Um desenho para esse problema é:
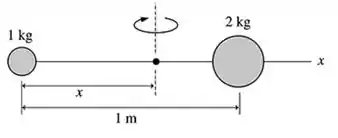
A nossa origem é o pontinho preto dessa imagem.
Passo 2
Para achar o torque podemos usar o momento de inercia, mas precisaremos achar o centro de massa antes. Então:
Centro de massa:
Passo 3
Cálculo do momento de inercia:
Para o a distância considerando a origem é
Para o a distância considerando a origem é
Então:
Passo 4
Finalmente podemos achar o Torque:
O é a frequência angular de 20 , como temos o tempo em segundos , devemos converter a frequência angular para r.
Assim: