Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 38

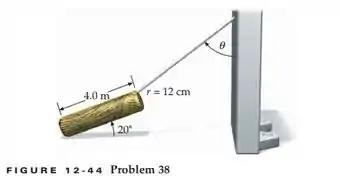
Uma tora homogênea , de 100 k g de massa, 4,0   m de comprimento e 12   c m de raio, é mantida em uma posição inclinada como mostrado na Figura 12-44. O coeficiente de atrito estático entre a tora e a superfície é 0,60 . A tora está na iminência de escorregar para direita. Determine a tração no cabo que a sustenta e o ângulo que ele forma com a parede vertical.

Passo 1

Pelo enunciado, temos que determinar a tração de modo que a tora fique em equilíbrio. As condições para um corpo rígido ficar em equilíbrio são:

∑ F → = 0

E

∑ τ → = 0

Olha essa ilustração aqui embaixo:

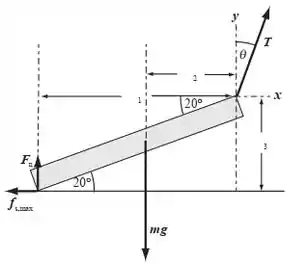
Passo 2

Vamos primeiro garantir que ∑ F → = 0 . No eixo x , temos:

∑ F x = T ⋅ s e n θ - f s ,   m a x = 0

Como f s ,   m a x = μ s F n :

T ⋅ s e n ( θ ) = μ s F n     ( i )

Agora para o eixo y :

∑ F y = T ⋅ cos ⁡ θ + F n - m g = 0

Logo,

T ⋅ cos ⁡ θ + F n = m g     ( i i )

Juntando i e ( i i ) :

s e n θ = μ s F n T

E

cos ⁡ θ = m g - F n T

Usando que s e n 2 θ + cos 2 ⁡ θ = 1 :

μ s F n 2   + m g - F n 2 = T 2

Passo 3

Agora vamos garantir que ∑ τ → = 0 . Fazendo torque com relação ao ponto onde T atua e considerando positivo no sentido horário:

m g ⋅ l 2 cos ⁡ 20 ° - f s ,   m a x ⋅ l s e n 20 ° - F n ⋅ l cos ⁡ 20 ° = 0     i i i

Como f s ,   m a x = μ s F n :

m g ⋅ l 2 cos ⁡ 20 ° - μ s F n ⋅ l s e n 20 ° - F n ⋅ l cos ⁡ 20 ° = 0

Assim,

F n = m g cos ⁡ 20 ° 2 μ s ⋅ s e n 20 ° + cos ⁡ 20 °

Substituindo os valores, temos:

F n = 100 k g ⋅ 9,81 N k g ⋅ cos ⁡ 20 ° 2 0,60 ⋅ s e n 20 ° + cos ⁡ 20 ° ≅ 402   N

Usando que μ s F n 2   + m g - F n 2 = T 2 :

T = 0,6 ⋅ 402 2 + 100 ⋅ 9,81 - 402 2 ≅ 627   N → T ≅   0,63   k N

Para calcular o ângulo θ :

s e n θ = μ s F n T = 0,6 ⋅ 402   N 0,63   k N = 0,38

Logo,

θ = a r c s e n 0,38 ≅ 22 °

Resposta

T ≅   0,63   k N

θ ≅ 22 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra uma viga vertical homogênea de comprimento L que está presa a uma dobradiça na extremidade inferior. Uma força horizontal F a é aplicada à viga a uma distância y da extremidade inferio
A Figura mostra uma viga horizontal homogênea, de massa m b e comprimento L , que é sustentada à esquerda por uma dobradiça presa a uma parede e à direita por um cabo que faz um ângulo θ com a horizon
Na figura, uma esfera de 10k g está presa por um cabo sobre um plano inclinado sem atrito que faz um ângulo θ = 45 ° com a horizontal. O ângulo φ é 25 º º. Calcule a tensão do cabo.
Depois de uma queda, um alpinista de 95k g está pendurado na extremidade de uma corda originalmente com 15m de comprimento e 9,6m m de diâmetro, que foi esticada de 2,8c m . Determine (a) a tensão, (b
Na figura, uma caçamba de 817k g está suspensa por um cabo A que, por sua vez, está preso no ponto 0 a dois outros cabos, B e C , que fazem ângulo θ 1 = 51,0 ° e θ 2 = 66,0 ° com a horizontal. Determi