Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 64
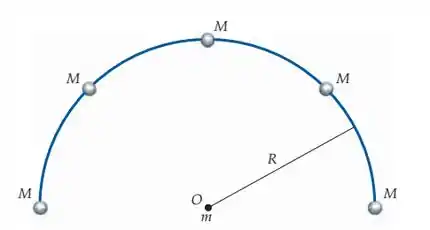
Cinco corpos, cada um de massa , estão igualmente espaçados sobre um arco de semicírculo de raio , como na figura. Um corpo de massa está localizado no centro de curvatura do arco. (a) Se é , é e é , qual é a força gravitacional sobre a partícula de massa devida aos cinco corpos? (b) Se o corpo de massa é removido, qual é o campo gravitacional no centro de curvatura do arco?
Passo 1
a) Vamos usar o princípio da superposição para calcular a força que atua na massa . Como assim? Isso quer dizer que vamos achar a força causada pela interação de com cada bola de massa , e dizer que a força total é a soma das forças de cada uma.
O módulo da força gravitacional gerada pela proximidade de uma massa com outra massa é
Sendo a distância entre elas.
Vamos calcular essa força de cada bola. Temos que. Já vai ser o mesmo para todas as massinhas e vale
Substituindo esses dados na nossa fórmulinha, temos:
Passo 2
Precisamos saber agora quanto valem as componentes horizontal e vertical de cada uma delas para que a gente possa somar.
Percebe que o ângulo entre cada segmento azul que liga a com é de . Para confirmar isso, é só você vê que temos 4 ângulos iguais em um intervalo de .
E repara também que a força gerada sempre vai tender juntar as duas massas, por isso temos as forças no sentido mostrado na figura.
Considerando um par habitual de eixos, com origem em , com positivo para a direita e positivo para cima, podemos colocar as forças em forma vetorial assim:
A força total será a soma de todas elas!
Substituindo o valor de
Essa é força sobre !
Passo 3
b) Ele quer no centro da curva. Como a força gravitacional é dada por
E já temos no centro da curva e da massinha no centro da curva, podemos Isolar e substituir nossos dados