Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 54
Uma bola é disparada por uma arma de ar comprimido com duas vezes o valor de sua velocidade terminal.
a. Qual será a aceleração inicial da bola, como um múltiplo de g, se ela for disparada diretamente para cima?
b. Qual será a aceleração inicial da bola, como um múltiplo de g, se
ela for disparada diretamente para baixo?
c. Desenhe um gráfico velocidade versus tempo plausível para a
bola disparada diretamente para baixo.
Passo 1
Fala aí! Bora começar pela letra A, considerando o eixo y positivo pra baixo. A gente tá ligado que as forças que vão agir na bolinha são a força gravitacional e a força de arrasto. Então, a segunda lei de Newtinho fica assim:
Mas se liga que o enunciado tá falando que a velocidade inicial é 2 vezes a velocidade terminal. Então nossa equação fica assim:
E a velocidade terminal é a velocidade limite (aceleração igual a zero). A gente pode calcular ela assim:
Vamos substituir na nossa equação
Logo
Positiva, pois a aceleração está pra baixo, assim como o sentido que adotamos para o eixo y.
Agora vamos pro item b!!
Passo 2
No item b, o que muda é o sentido da força de arrasto, que, como sempre, é contra a trajetória. Aí fica assim:
Fora isso, a gente vai fazer exatamente os mesmos passos de antes, que vai resultar em
Obs: negativo, pois adotamos a trajetória positiva pra baixo, e nesse caso a aceleração tá contra o movimento (pra cima).
Passo 3
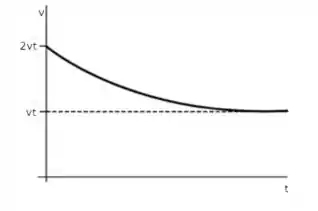
Por último, precisamos esboçar o gráfico de velocidade x tempo da bolinha disparada pra baixo!
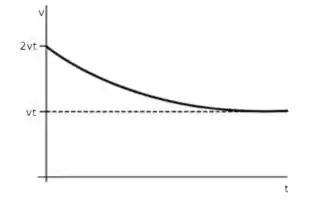
A bola vai começar bem rápido (2vt) mas vai perdendo velocidade até chegar na velocidade terminal (vt), já que este é o limite, devido a força de arrasto.
Resposta
- a=5g
- a=-3g
