Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 77
Uma bola é lançada do nível do chão e volta ao chão, no mesmo nível, 2,44 s após, a uma distância de 40,0 m do ponto de lançamento. Encontre a magnitude do vetor velocidade inicial e o ângulo que ele forma acima da horizontal. (Ignore a resistência do ar.)
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. Percebe que ele está falando de um movimento de lançamento de projetil porque temos movimento para cima e para frente, só que nosso projeitil é uma bola.
Nesse movimento, o que acontece verticalmente independe do que acontece horizontalmente. No movimento vertical temos um movimento de aceleração constante. E no horizontal temos velocidade constante.
A figura abaixo retrata o movimento do enunciado:
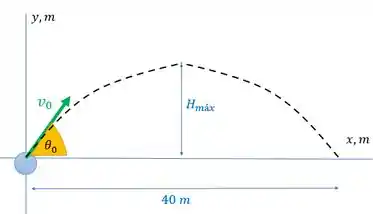
E ele diz que a bola faz esse movimento em .
O problema nos pede o ângulo de lançamento do projétil e a velocidade inicial. A velocidade inicial tem como componentes a velocidade inicial vertical e a velocidade inicial horizontal .
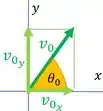
Então para achar o módulo de , podemos usar a fórmulinha de módulo:
E para achar a orientação de podemos usar a fórmulinha do ângulo que orienta um vetor a partir de suas componentes:
Então precisamos achar e . Bora lá!
Passo 2
O movimento na horizontal tem velocidade constante. Então é a velocidade de todo o movimento. Como a gente tem o tempo que o movimento dura e o alcance horizontal, a gente pode usar a fórmula da velocidade média pra achar . Assim:
Passo 3
Agora vamos achar a velocidade vertical. Temos o tempo decorrido em todo o percurso. Aí a gente pode lembrar de duas coisas.
A primeira é que o tempo que a bola leva para subir é o mesmo que a bola leva para descer, assim, o tempo de subida seria
E outra coisa que a gente pode lembrar é que na altura máxima (o ponto final desse tempo de subida), a velocidade vertical é nula.
Com essas informações, a gente pode achar a velocidade vertical inicial usando essa equação aqui para o movimento de aceleração constante:
No nosso caso, (negativa porque ela aponta para baixo). Substituindo isso, nosso de subida e :
Passo 4
Agora podemos encontrar o valor da velocidade inicial e do ângulo de lançamento:
E agora o ângulo: