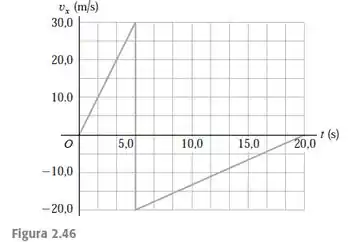
Uma bola rígida, que se move em linha reta (o eixo x), bate em uma parede e repentinamente ricocheteia por um breve instante. O gráfico na Figura 2.46 mostra a velocidade dessa bola
em função do tempo. Nos primeiros desse movimento, determine a) A distância total percorrida pela bola e b) Seu deslocamento. c) Faça um gráfico axt para esse movimento da bola. d) O gráfico apresentado é realmente vertical a ? Explique.
Passo 1
Bora analisar o gráfico:
Quando temos uma linha reta a aceleração é constante, então esse movimento consiste em
dois segmentos de aceleração constantes e as equações de aceleração constantes podem ser usadas para cada um desses segmentos.
Podemos observar que no intervalo de tempo de a , a velocidade, , é positiva e a bola se move na direção positiva do gráfico, sendo .
Para o intervalo de tempo a , a velocidade, , é negativa e a bola se move na direção .
A aceleração, , é a inclinação do gráfico.
Passo 2
Agora vamos analisar os dados:
- de a :
- de a :
Passo 3
- Para calcular a distancia total, vamos calcular a distancia que cada um deles percorreu e depois soma-las, pela seguinte relação:
- Quanto ao deslocamento, temos que:
- de a :
- A bola está em contato com o chão por um período de tempo pequeno, mas diferente de zero, e a direção da velocidade não muda instantaneamente. Então, não, o gráfico real de não é realmente vertical em .
Note que na distância da 2 temos um numero negativo, e calculamos ele como positivo na distancia total. O fato é que ele se dá por negativo porque temos uma velocidade negativa, mas sabemos que não podemos ter distancia negativa.
Passo 4
O que significa que a bola termina na direção negativa , ou seja, do ponto de onde começou.
Passo 5
a :
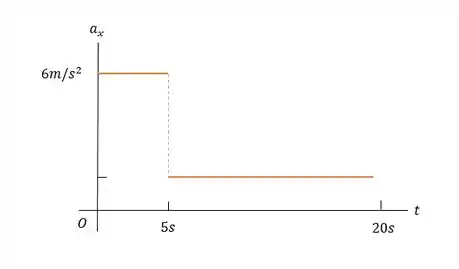
Passo 6
Resposta
-
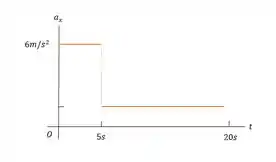
- Não.