Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.10 - Ex. 65

A Fig. 10-45 mostra um corpo rígido formado por um aro fino (de massa m e raio R   =   0,150   m ) e uma barra fina radial (de massa m e comprimento L   =   2,00   R ). O conjunto está na vertical, mas se recebe um pequeno empurrão, começa a girar em tomo de um eixo horizontal no plano do aro e da barra, que passa pela extremidade inferior da barra. Supondo que a energia fornecida ao sistema pelo pequeno empurrão é desprezível, qual é a velocidade angular do conjunto ao passar pela posição invertida (de cabeça para baixo)?

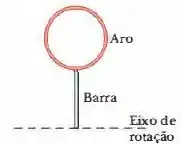
Passo 1

Pessoal, antes de tudo , vamos escrever o I a r o C M     e     I b a r r a C M :

Temos que L=2R e :

I a r o C M   = m R ² 2 e I b a r r a C M = m L ² 12

Agora vamos escrever a equação do momento de inércia:

I r =   I a r o   + I B a r r a

Para fazer este cálculo vamos aplicar o teorema dos eixos paralelos. Primeiro no aro para descobrir   I a r o   :

  I a r o   = I a r o C M   + m d ²

Se observarmos a figura, a distância entre o eixo (a base da haste) até o centro de massa do arco (centro do aro) e de d = L + R e podemos substituir esse valor no teorema:

  I a r o   = I a r o C M   + m d ²

  I a r o   = I a r o C M   + m ( R + L ) ²

  I a r o   = m R ² 2 + m ( R + L ) ²

Como L=2R

  I a r o   = m R ² 2 + m ( 3 R ) ²

  I a r o   = m R ² 2 + 9 m R ²

  I a r o   = 9,5 m R ²

Agora aplicamos o teorema dos eixos paralelos para a barra:

  I b a r r a   = I b a r r a C M   + m d ²

Se observarmos a figura o valor da distância do eixo (base da barra) até seu centro de massa (metade da barra) é d = L 2 e podemos substituir esse valor no teorema:

  I b a r r a   = I b a r r a C M   + m d ²

  I b a r r a   = I b a r r a C M   + m ( L 2 ) ²

  I b a r r a   = m L ² 12 + m ( L 2 ) ²

  I b a r r a   = m L ² 12 + m L ² 4

  I b a r r a   = m L ² 3

Como L=2R

  I b a r r a   = m ( 2 R ) ² 3

  I b a r r a   = 4 m R ² 3

Agora Temos tudo que precisamos para calcular o momento de inércia:

I r =   I a r o   + I B a r r a

I r = 9,5 m R ² + 4 m R ² 3

I r = 10,83 m R ²

Passo 2

Vamos agora calcular o centro de massa do conjunto pois usaremos ele na conservação de energia mais adiante.

Primeiro vamos calcular a altura do centro de massa

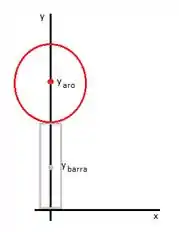
Para calcular a altura do centro de massa ( y C M ) vamos usar a seguinte fórmula:

y C M = y a r o * m b a r r a + y b a r r a . * m a r o m a r o + m b a r r a

y C M =   ( R + L ) m + ( L 2 ) m 2 m

y C M = ( R + 2 R ) m + ( 2 R 2 ) m 2 m

y C M = 3 R + R 2

y C M = 2 R

Passo 3

Agora temos tudo que precisamos para aplicar a lei de conservação de energia. Vamos observar no desenho a altura do centro de massa no início ( h C M i ) quando o aro estava em pé e em repouso e a altura do centro de massa no fim ( h C M i ), com o aro para baixo e tendo uma certa velocidade angular ( ω f ) que queremos encontrar:

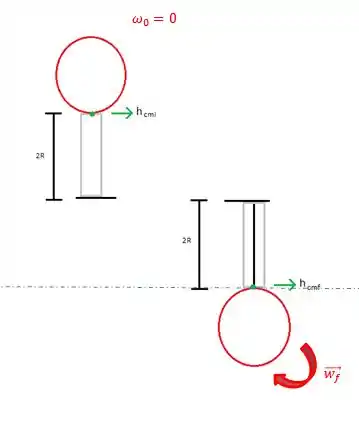
Sabemos que:

E i =   E f

K i +   U g C M i = K f + U g C M f  

Se considerarmos que o nosso eixo de referência está na altura h c m f , temos que caso K i e U g C M f são nulos, então:

E i =   E f

  U g C M i = K f

m g h C M i = I r ω f 2 2

( 2 m ) g ( 4 R ) = 10,83 m R ² ω f 2 2

ω f 2 = 2 * 4 * 2 g 10,83 R

ω f = 16 * 9,8 10,83 * 0,15

ω f = 9,82   r a d / s

Resposta

ω f = 9,82   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois discos metálicos, um com raio R 1 = 2,50 c m e massa M 1 = 0,80 k g e o outro com raio R 2 = 5,0 c m e massa M 2 = 1,60 k g , são soldados juntos e montados em um eixo sem atrito passando pelo ce
No cilindro junto com a massa do Exemplo 9.9 (Seção 9.4), suponha que a massa m que cai seja feita de borracha, de modo que nenhuma energia mecânica é perdida quando a massa atinge o solo. a) Supondo
Uma barra uniforme de comprimento L repousa sobre uma superfície horizontal sem atrito. A barra possui um pivô, de modo que ela pode girar sem atrito em torno de um eixo passando por uma das suas extr
Considere uma transição de um estado mais baixo de energia para um estado mais alto – isto é, a absorção de um quantum de energia, resultando em um aumento da energia rotacional em uma molécula de N 2
Mostre que a diferença de energia entre um nível rotacional de uma molécula e o nível próximo mais alto é proporcional a l + 1 .