Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 3.Problemas - Ex. 13
Uma bolinha homogênea de massa e raio rola sem deslizar sobre uma calha cilíndrica de raio , na vizinhança do fundo, ou seja, com . Mostre que o movimento é harmônico simples e calcule a frequência angular..
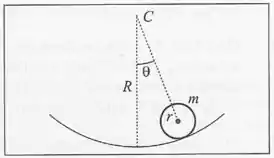
Passo 1
As únicas forças que agem sobre a bolinha são o seu próprio peso e a força de atrito.
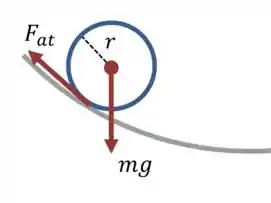
Já que a força peso age no centro de massa, a única força que produz torque para que a bolinha role sem deslizar é o atrito:
Onde é a aceleração angular da bolinha, em torno do seu próprio eixo. O momento de inércia da esfera em relação ao seu centro é:
Então:
Beleza, já temos a fórmula da força de atrito.
Passo 2
Agora temos que aplicar a segunda lei de Newton sobre o a bolinha. Vamos analisar apenas a direção tangencial, então temos que pegar apenas uma componente do peso:
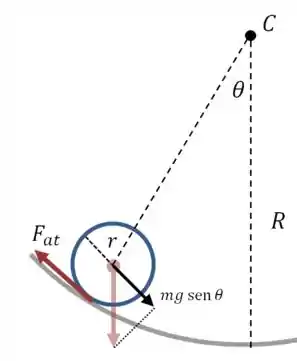
O sinal negativo aparece na força peso porque ela faz com que diminua. Vamos reescrever a aceleração em função do ângulo :
Estamos aproximando a distância do centro de massa até o ponto como :
Agora vamos dividir tudo por e aproximar :
Passo 3
O problema agora é que ainda temos duas variáveis. Precisamos dar um jeito de escrever em função de . Dê uma olhada no desenho:
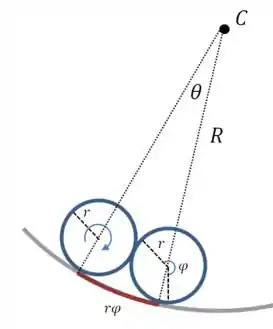
Derivando duas vezes:
Então:
Que é a equação de um movimento harmônico simples, e a frequência angular é:
Resposta
O movimento é harmônico simples e a frequência angular é .