Uma lâmpada pendurada no teto do vagão de um trem oscila com um período quando o trem está em repouso. O período será (ligue as colunas da esquerda com as da direita)

1. Maior que quando

2.Menor que quando

3.igual a quando

1. O trem se move horizontalmente com velocidade constante
2. O trem faz uma curva com módulo da velocidade constante
3. O trem sobe um morro com módulo da velocidade constante
4. O trem passa sobre a crista de um morro com o módulo da velocidade constante

No caso 1, vemos uma nova força agindo sobre o sistema, a centrípeta, que permite que o vagão faça o movimento da curva. Essa força gera uma aceleração no teto, fazendo com que o período da lâmpada seja maior por causa da inércia.

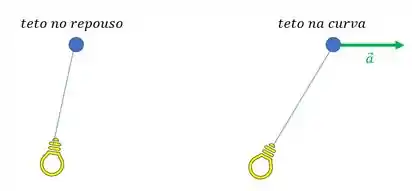
Assim, o período será maior quando o trem faz uma curva com módulo da velocidade constante (letra B), pois quando o trem entra na curva, a lâmpada se deslocará mais para o lado de fora da curva.

No caso 2, temos uma força centrípeta também, para que o vagão passe pelo cume do morro. A aceleração centrípeta no cume do morro vai apontar para baixo. Deixando o vagão sob duas acelerações verticais par abaixo, a aceleração da gravidade e a aceleração centrípeta.

Isso faz com que a aceleração para baixo sob o pêndulo aumente, diminuindo o seu período. É o como se o efeito da gravidade sobre o pêndulo aumentasse.

Ou seja, o período será menor quando o trem passa pela crista do morro com módulo de velocidade constante (letra D), pois a aceleração do trem será para dentro do morro, que ao ser somado com a gravidade, faz com que o período fique menor (já que ele é inversamente proporcional ao efeito da gravidade).

E no caso 3, o período será igual quando o trem está com velocidade constante, ou seja, num movimento retilíneo uniforme (letra A).

Isso porque a aceleração sobre o sistema quando ele está em repouso e quando ele está em velocidade constante no movimento retilíneo é a mesma: somente a gravidade.