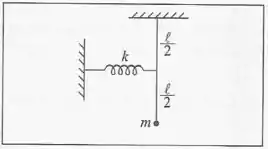
O pêndulo da figura, formado por uma barra de massa desprezível e comprimento com uma massa suspensa, está ligado em seu ponto médio a uma mola horizontal de massa desprezível e constante elástica , com a outra extremidade fixa e relaxada quando o pêndulo está em equilíbrio na vertical. Calcule a frequência angular de pequenas oscilações no plano vertical.
Passo 1
Vamos escrever uma equação para o torque resultante em torno do ponto de suspensão:
As duas forças que realizam torque sobre o pêndulo são o peso da massa e a força da mola.
A componente tangencial do peso é dada por , e age a uma distância do ponto de suspensão:
E o sinal negativo aparece porque o peso aponta no sentido que reduz o ângulo .
Passo 2
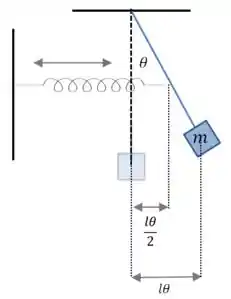
Já a força da mola é dada pela lei de Hooke, e age a uma distância do ponto de suspensão:
E podemos escrever em função de para pequenas oscilações:
Então o torque resultante é:
Aproximando mais uma vez:
Passo 3
Agora vamos completar a equação do torque resultante.
Temos uma massa a uma distância do ponto de suspensão, então o momento de inércia é:
Substituindo na equação de cima:
Que é a equação de um oscilador harmônico com a seguinte frequência angular:
Resposta
A frequência angular de pequenas oscilações é .