Um brinquedo em um parque de diversões consiste em carrinhos em forma de avião ligados por cabos de aço (Figura 11.63). Cada cabo possui um comprimento igual a 15,0 m e área da sua seção reta igual a .

a) Ache a dilatação do cabo quando o carrinho está em repouso. (Suponha que o peso total de cada carrinho juntamente com dois passageiros seja igual a 1900 N.)

b) Quando o brinquedo está em movimento, o carrinho gira com velocidade angular máxima de 8,0 rev/min. Qual é a dilatação do cabo nesse caso?

Fala aí! como vai?

Nesse problema temos um brinquedo em um parque de diversões que consiste em carrinhos em forma de avião ligados por cabos de aço. Cada cabo possui um comprimento igual a 15,0 m e área da sua seção reta igual a .

A partir daí queremos saber qual a dilatação do cabo quando o carrinho está em repouso e tambem quando o brinquedo está em movimento, o carrinho gira com velocidade angular máxima de 8,0 rev/min.

Tem ideia de como fazemos isso?

utilizaremos o módulo mais conhecido como módulo de Young (Y) para solucionarmos o problema. Mas antes, vamos analisar: quando o carro está parado, a tensão na haste é o peso de 1900 N do carro e dos ocupantes; quando ele está em movimento, a tensão na haste é dada por .

O diagrama que representa a situação é dado por

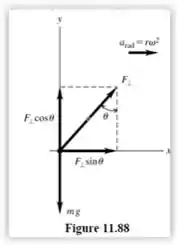
O carro viaja em um círculo de raio , onde l é o comprimento da haste e θ é o ângulo que a haste faz com a vertical. Para o aço, e .

Veja só!