Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.3 - Ex. 46

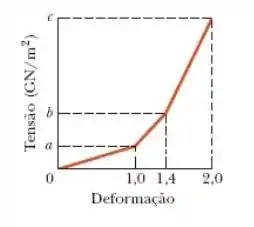
A figura mostra o gráfico tensão-deformação aproximado de um fio de teia de aranha, até o ponto em que se rompe com uma deformação de 2,00 . A escala do eixo das tensões é definida por a   =   0,12   G N / m 2 ,   b   =   0,30   G N / m 2 e c   =   0,80 G N m 2 .   Suponha que o fio tem um comprimento inicial de 0,80   c m , uma área da seção reta inicial de 8,0 × 10 - 12 m 2 e um volume constante durante o alongamento. Suponha também que quando um inseto se

choca com o fio, toda a energia cinética do inseto é usada para alongar o fio. (a) Qual é a energia cinética que coloca o fio na iminência de se romper? Qual é a energia cinética (b) de uma drosófila com uma massa de 6,00   m g voando a 1,70   m / s e (c) uma abelha com uma massa de 0,388   g   voando a 0,420   m / s ? O fio seria rompido (d) pela drosófila e (e) pela abelha?

Passo 1

(a)Belezoca galerinha, vamos considerar que todo o trabalho W usado para deformar o fio é transformado em energia cinética E c i n . Então temos que:

W = E c i n

Mas como calcular W ?

Se liga só, por definição, o trabalho de uma força exercida na direção x é definido por:

W = ∫ F x d x

Mas agora que começa a malandragem, porque podemos lembrar das relações entre tensão e força, onde a tensão resutante de uma força F x que atua sobre uma superfície A , pode ser dada como:

Tensão = F x A 0

Onde A 0 é dado pra gente como área da seção reta inicial, A 0 = 8,0 × 10 - 12   m 2 , logo:

F x = A 0 × Tensão

Além disso, temos que o alongamento d x é dado pela deformação vezes o comprimento L , logo:

d x = L × deformação

Substituindo essas informações na integral, obtemos:

W = ∫ A 0 × Tensão L × deformação

Sendo assim, temos que:

W = A 0 L ∫ Tensão deformação

Passo 2

Iradoso, a relação final do Passo 1 nos mostra um resultado importante: o trabalho é dado pelo produto da área de seção reta do fio pelo comprimento dele e pela área sob a curva Tensão × Deformação . Calculando a área sob o gráfico da imagem do enunciado, a gente encontra:

Á r e a = 1,0 × a 2 + b + a × 0,4 2 + c + b × 0,6 2

Á r e a = 4,74 × 10 8   N/m²

Então assim:

W = 4,74 × 10 8 N/m² × 0,008   m × 8,0 × 10 - 12   m 2

W = 3,03 × 10 - 5   J = E c i n

Passo 3

(b)Da relação última encontrada no passo 2, vem, sabendo que m e v são a massa e a velocidade da drosófila:

E c i n = 1 2 m v 2

E c i n = 1 2 6,00 × 10 - 6   kg 1,70 m/ s 2

E c i n = 8,67 × 10 - 6 J

Passo 4

(c) Contabilizando a energia cinética da abelha, temos:

E c i n = 1 2 3,88 × 10 - 4   kg 0,420   m/s 2

E c i n = 3,42 × 10 - 5   J

Passo 5

(d) Nesse caso, a energia cinética encontrada da drosófila,   8,67 × 10 - 6 J , não é suficiente para romper o fio, pois ela é menor que W .

Passo 6

(e)Como a energia cinética da abelha, 3,42 × 10 - 5 J ,   é maior do que o trabalho necessário para romper o fio, W , a gente pode concluir que a abelha rompe o fio.

Resposta

(a)   3,03 × 10 - 5 J

(b)   8,67 × 10 - 6 J

(c) 3,42 × 10 - 5 J

(d)Não

(e)Sim

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fabricante de álcool clandestino produz etanol puro (álcool etílico) durante a madrugada e o acumula em um tanque de aço inoxidável em forma de cilindro com diâmetro igual a 0,300 m tampado na part
Lei de Hooke para um cabo. Um cabo de comprimento l 0 e área de seção reta A suspende um peso W. a) Mostre que, se o cabo obedecer à Equação (11.7), ela se comportará como uma mola de força constante
Um eixo de bronze possui comprimento de 1,40 m e a área de sua seção reta é igual a 2,0c m 2 . Ele é ligado à extremidade de um eixo de níquel de comprimento L e área da seção reta igual a 1,0c m 2 .
Um corpo de massa 12,0 kg, amarrado à extremidade de um fio de alumínio que possui comprimento inicial de 0,50 m, é enrolado em um círculo vertical que gira com velocidade constante de 120r e v / m i
Você pendura um refletor pela extremidade de um fio de aço vertical. O refletor produz uma dilatação de 0,18 mm no fio, e a tensão é proporcional à deformação. Qual seria a dilatação a) se fio tivesse