Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.3 - Ex. 45

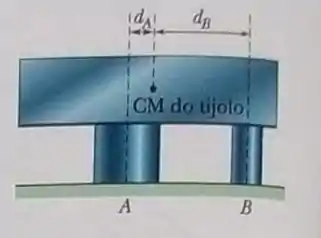
Na figura, um tijolo de chumbo repousa horizontalmente sobre os cilindros A e B . As áreas das faces superiores dos cilindros obedecem à relação A A = 2 A B ; os módulos de Young dos cilindros obedecem à relação E A =   2 E B . Os cilindros tinham a mesma altura antes que o tijolo fosse colocado sobre eles. Que fração da massa do tijolo é sustetada (a)pelo cilindro A e (b) pelo cilindro B ? As distâncias horizontais entre o centro de massa do tijolo e os eixos dos cilindros são d A e d B . (c) Qual é o valor da razão d A d B ?

Passo 1

(a)Falaaa galerinha bonita, pra gente fazer esse exercício aqui, primeiro precisamos perceber que os cilindros sofrem a mesma variação de comprimento, pois o tijolo permanece na posição vertical. Lembrando da relação que determina o módulo de Young

E = F A Δ l l 0

Temos, sabendo que os deslocamentos e os comprimentos iniciais de A e de B são iguais:

Δ l l = F A A A E A = F B A B E B

Passo 2

Da relação anterior, temos:

F A = F B A B E B × E A A A = F B A A 2 E A / 2 × E A A A = 4 × F B

Além disso, como ambos suportam o peso W do tijolo:

F A + F B = W

Então:

5 F B = W

F B = W 5

Consequentemente, F A = 4 W 5 e F A W = 0,80

Passo 3

(b)Assim como vimos há pouco, F B W = 1 5 = 0,20

Passo 4

(c)Do equilíbrio de torques com relação ao centro de massa, temos:

F A × d A = F B × d B

Então:

d A d B = F B F A = 0,25

Resposta

(a)   0,80

(b) 0,20

(c) 0,25

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de bronze deve sustentar uma força de tensão de 350 N sem se romper. Qual deveria ser seu diâmetro mínimo?
Um fio de aço de comprimento igual a 4,0m possui uma seção reta com área de 0,050c m 2 . Seu limite de proporcionalidade possui um valor 0,0016 vezes seu módulo de Young (Tabela 11.1 ). Sua tensão de r
Um fio metálico, que possui comprimento de 3,50 m e diâmetro igual a 0,70 mm, foi submetido ao seguinte teste. Uma carga pesando 20 N foi inicialmente presa ao fio para mantê-lo esticado. A posição da
Um eixo de 1,05 m de comprimento e peso desprezível é suportado em suas extremidades por fios A e B de comprimentos iguais (Figura 11.62). A área da seção reta de A é igual a 2,0 m m 2 e a de B é igua
Uma barra com área da seção reta A é submetida a forças de dilatação iguais e opostas em suas extremidades. Considere um plano ao longo da barra formando um ângulo θ com o plano da barra (Figura 11.64