Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.3 - Ex. 47

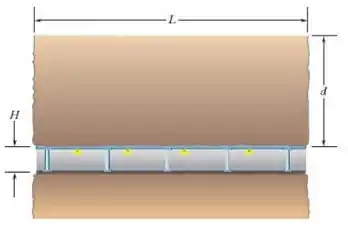
Um túnel de comprimento L   =   150   m , altura H   =   7,2   m , largura de 5,8   m e teto plano deve ser construído a uma distância d   =   60   m da superfície. O teto do túnel deve ser sustentado inteiramente por colunas quadradas de aço com uma seçao reta de 960   c m 2 . A massa de 1,0   c m 3 de solo é 2,8 g (a) Qual é o peso total que as colunas do túnel devem sustentar? (b) Quantas colunas sao necessárias para manter a tensao compressiva em cada coluna na metade do limite de ruptura?

Passo 1

(a)Show de bolinhas pessoal, a questão nos pede para determinar o peso total que as colunas do túnel devem sustentar. Perceba que temos três informações importantes aqui: a área do teto plano (tirada a partir de suas dimensões) e sua massa específica. Então, para calcularmos esse peso, podemos fazer:

P = m g

P = ρ V g

Logo:

P = ρ A × d 9,8   m/s²

P = 2800   kg/m³ 870   m 2 × 60   m 9,8   m/s²

P = 1,4 × 10 9   N

Passo 2

(b) O número de colunas pode ser obtido assim:

Primeiro, precisamos lembrar que T e n s ã o = F o r ç a Á r e a . Nesse caso, deseja-se manter a tensão em cada coluna igual à metade do limite de ruptura do aço, igual a 400 × 10 6   N/m² . Então, temos que T e n s ã o = P e s o t o t a l n × Á r e a   d e   c a d a   c o l u n a , tal que:

1 2 × 400 × 10 6 N/m² = 1,4 × 10 9   N n × 960 × 10 - 4   m 2

n = 2 × 1,4 × 10 9   N 400 × 10 6 N/m² × 960 × 10 - 4   m 2

A partir disso, encontramos que:

n ≅ 7 5

Resposta

(a)   1,4 × 10 9   N

(b)   7 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa quadrada de aço possui 10,0 cm de lado e 0,500 cm de espessura. a) Ache a tensão de cisalhamento resultante quando uma força de módulo 9,0 × 105 N é aplicada a cada um dos quatro lados, para
Uma amostra de óleo com volume inicial de 600 cm3 é submetida a um aumento de pressão de 3,6 × 106 Pa, e o volume diminui de 0,45 cm3. Qual é o módulo de compressão do material? Qual é a sua compressi
Forças de cisalhamento são aplicadas a um sólido retangular. As mesmas forças são aplicadas a outro sólido com o mesmo material, porém as arestas possuem comprimentos três vezes maiores. Em cada caso
Um cabo de aço, cuja área da seção reta é igual a 3,0 cm2, possui limite elástico igual a 2,40 × 10^8 Pa. Calcule a aceleração máxima de baixo para cima que este cabo pode suportar, quando ele for usa
Em um laboratório de teste de materiais, um fio metálico fabricado com uma liga nova se rompe quando uma força de tensão de dilatação de 90,8N é aplicada perpendicularmente a cada uma das suas extremid