Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 15

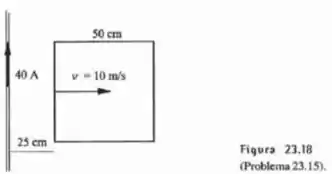
O cabo (longo) que transporta a corrente na Figura 23.18 está no mesmo plano da espira quadrada, a qual também se move naquele plano. O fio da espira tem resistência de 30   m Ω . Calcule a corrente na espira.

Passo 1

Fala pessoal, tudo tranquilo?

Nesse exercício queremos saber a corrente induzida na espira. Para isso, primeiro escrever uma expressão para o fluxo magnético sobre ela.

Vamos considerar uma faxinha vertical na espira de largura d r a uma distância r do fio:

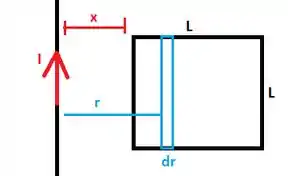
No desenho, x é a distância da extremidade esquerda da espira ao fio. O fluxo d Φ B sobre essa faxinha vai ser o produto do campo (que vai entrar dentro da tela) pela área L   d r :

d Φ B = B r ⋅ L   d r

Mas a expressão do campo do fio infinito é

B r = μ 0 I 2 π r

Assim,

d Φ B = μ 0 I L 2 π ⋅ d r r

Para achar o fluxo total basta integrar de r = x até r = x + L :

Φ B = μ 0 I L 2 π ∫ x x + L d r r = μ 0 I L 2 π ln ⁡ x + L x

Ou ainda,

Φ B = μ 0 I L 2 π ln ⁡ 1 + L x

Eu não me preocupei muito com o sinal do fluxo nem com para onde aponta o versor normal à espira. Estamos interessados apenas com o módulo das grandezas...

Passo 2

Usando a lei de Faraday podemos achar a fem:

E = - d Φ B d t = - μ 0 I L 2 π ⋅ 1 1 + L x ⋅ d d t L x

Observe que

d d t L x = - L x 2 ⋅ d x d t

Aqui vem o pulo do gato:

v = d x d t

Com isso, temos

E = μ 0 I L 2 π ⋅ x x + L ⋅ L x 2 ⋅ v = μ 0 I L 2 v 2 π x x + L

Passo 3

Para terminar basta chamar a lei de Ohm:

E = R I i n d

Assim,

I i n d = μ 0 I L 2 v 2 π R x x + L

Substituindo μ 0 = 4 π ⋅ 10 - 7   T m / A , L = 50   c m , x = 25   c m , R = 0,030   Ω , I = 40   A e v = 10   m / s , encontramos:

I i n d = 3,6 ⋅ 10 - 3   A

Resposta

I i n d = 3,6 ⋅ 10 - 3   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a altura acima da superfície da Terra onde o módulo do campo magnético da Terra cai à metade do valor na superfície, na mesma latitude magnética. (Use a aproximação do campo do dipolo dada no
Dois fios paralelos ao eixo z e separados por uma distância de 4r transportam correntes iguais t, em sentidos opostos, como mostra a Fig. 34-21. Um cilindro circular, de raio r e comprimento L. tem se
No Exemplo 34-3. encontramos para o componente vertical do campo magnético da Terra em Tucson, Arizona, o valor de 43 μ T. Supondo que este seja o valor médio em todos os pontos do Arizona, cuja área
Enrolamos uma folha de papel formando uma superfície cilíndrica e, a seguir, colocamos esta superfície nas proximidades de uma barra imantada, como mostra a Fig. 34-20. (a) Esboce as linhas de campo B
Use os resultados do Problema 13 para calcular o campo magnético da Terra (módulo e inclinação): (a) no equador magnético; (b) num ponto de latitude magnética igual a 60°; (c) no polo norte magnético.