Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 06

Em cada um dos diagramas de corpo livre, as forças são exercidas sobre um objeto de 2,0 kg. Para cada diagrama, determine os valores de a x e a y , os componentes em x e em y da aceleração.

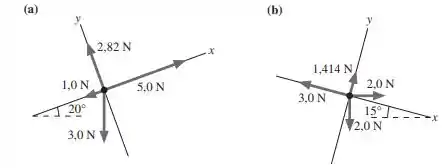
Passo 1

Seguindo o raciocínio do exercício anterior, podemos calcular:

a x = ∑ F x m                         a y = ∑ F y m

Note que a orientação dos eixos x e y nessa questão não segue a convenção usual de horizontal e vertical. Porém, nada muda (basta você imaginar a figura inteira rotacionando até que os eixos fiquem na horizontal e vertical).

Passo 2

Penso que a grande dificuldade de muitos alunos é “saber” onde colocar os ângulos. Na explicação a seguir, tentarei ser o mais claro possível quanto a isso. Lembre-se que nosso objetivo é decompor as forças nas direções x e y.

Passo 3

  1. Veja o esquema:

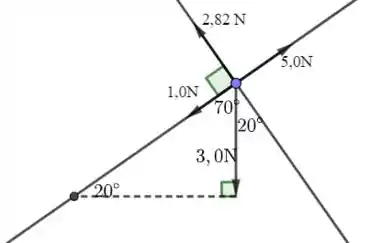
    2. Precisamos encontrar o ângulo que a força de 3,0 N faz com um dos eixos. No caso da figura, encontrei que o ângulo que a força faz com o eixo y é de 20°. Para encontrar tal ângulo, fechei o triângulo retângulo da figura, de modo a encontrar o ângulo de 70°. Logo após, basta usar o fato de que os eixos x e y são perpendiculares. Assim, 20° é o complementar de 70°.

    Encontrado o ângulo de 20°, podemos escrever que:

    1. Componente da força de 3,0 N em y: - 3,0   N cos ⁡ 20 ° (sinal negativo pois ela está para baixo);
    2. Componente da força de 3,0 N em x: - 3,0   N sin ⁡ 20 ° (sinal negativo pois ela está para a esquerda);

    Agora que todas as forças estão decompostas no eixo x e y, podemos escrever:

    a x = ∑ F x m = + 5,0   N + - 1 ,   0   N + - 3,0 sin ⁡ 20 ° N 2,0   k g = 1,5   m / s 2

    a y = ∑ F y m = + 2,82   N + - 3,0 cos ⁡ 20 °   N 2,0   k g = 0

    Passo 4

  2. Veja o esquema abaixo:

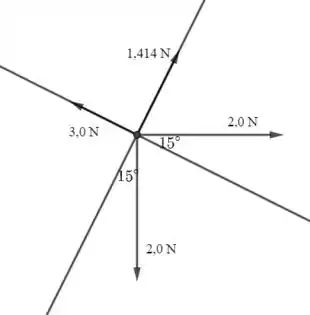
Assim, temos:

a x = ∑ F x m = + 2,0 cos ⁡ 15 °   N + + 2,0 sin ⁡ 15 °   N + - 3,0   N 2,0   k g = - 0,27   m / s 2

a y = ∑ F y m = + 1,414   N + + 2,0 sin ⁡ 15 ° + - 2,0 cos ⁡ 15 ° 2,0   k g = 0

Resposta

  1. a x = 1,5   m / s 2 ; a y = 0 .
  2. a x = - 0,27   m / s 2 ; a y = 0 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas forças horizontais F → 1 e F → 2 agem sobre um disco de 4,0k g que desliza sem atrito sobre o gelo, no qual foi desenhado um sistema de coordenadas x y . A força F → 1 aponta no sentido positivo
Uma partícula de 0,340k g se move no plano x y de acordo com as equações x ( t )=- 15,00+2,00 t-4,00 t 3 e y ( t )=25,00+ 7,00 t-9,00 t 2 , com x e y em metros et em segundos . No instante t=0,700s ,
Duas forças agem sobre a caixa de 2,00k g vista de cima na Fig. 5-31, mas apenas uma é mostrada. Para F 1=20,0N , a= 12,0 m s 2 e θ=30,0 ° , determine a segunda força (a) em termos dos vetores unitári
Qual é o módulo da força necessária para acelerar um trenó-foguete de 500k g até 1600k m / h em 1,8s , partindo do repouso?
Um carro a 53k m / h se choca com um pilar de uma ponte. Um passageiro do carro se desloca para a frente de uma distância de 65c m (em relação à estrada) até ser imobilizado por um airbag inflado. Qua