Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 62
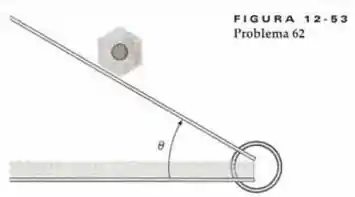
Um lápis sextavado é colocado sobre um caderno (Figura 12-53). Determine o menor coeficiente de atrito, tal que, se a capa do caderno for erguida, o lápis rolará para baixo sem escorregar.
Passo 1
Então gente, para resolver este problema nós temos que colocar as forças que vão atuar neste corpo enquanto ele está no limite do rolamento.
A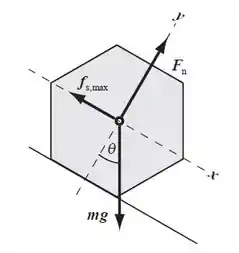
No centro de gravidade, ou seja, no ponto central do hexágono, temos a força gravitacional sendo aplicada para baixo. Dada por:
É importante percebermos que a força peso passa pelo vértice, porque quando ele está na iminência de rolar o lápis ficará apoiado somente neste ponto! Assim, se quisermos que o lápis fique na iminência de rolar sem escorregar estes dois pontos por uma reta vertical. E nessa situação as condições de equilíbrio ainda serão válidas.
Bem legal, né ?!
Como nós temos duas superfícies em contato, existe a força normal perpendicular à superfície, que neste caso é a capa do caderno, e a força de atrito , ou seja, a menor força de atrito necessária para que o corpo saia do repouso.
No caso da iminência do movimento, estas duas forças se relacionam:
Agora ficou fácil ! Como as condições de equilíbrio ainda se aplicam só precisamos fazer o somatório das forças e achar o coeficiente de atrito mínimo para que o corpo se mova.
Passo 2
Vamos começar usando a primeira condição. Se , então .
Quando observamos as forças, a força peso faz um ângulo com eixo y, obtemos isso fazendo uma manipulação matemática bem rápida. Se observarmos a geometria do hexágono:
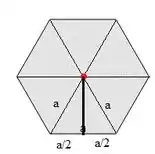
O hexágono é formado por 6 triângulos equilátero, ou seja, possui os três ângulos iguais a 60° e os três lados iguais, a. O ângulo então pode ser calculado pelo triângulo retângulo formado na figura:
Agora que temos estes dados podemos calcular a força peso na direção x e y:
Muito bem ! já sabemos todas as forças atuantes no corpo em ambas as direções.
Passo 3
Agora só nos resta fazer o somatório ! Separando na direção x nós temos a força peso na direção x e a força de atrito, com sentidos opostos:
Substituindo
Isolando
Na direção y, temos a força da gravidade para baixo e a força normal voltada para cima:
Substituindo :
Substituindo em
Ou seja, o atrito deve ser maior ou igual a para que haja movimento.