Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.3 - Ex. 32
Uma caixa de laranjas de está sendo empurrada ao longo de um piso horizontal. À medida que ela se move, sua velocidade diminui a uma taxa constante de a cada segundo. A força aplicada possui componente horizontal de e um componente vertical de de cima para baixo. Calcule o coeficiente de atrito cinético entre a caixa e piso.
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
O enunciado pediu pra gente calcular o coeficiente de atrito cinético entre a caixa e o piso, sabendo que ela tem o peso e está se movendo com uma desaceleração , por meio da aplicação de uma força . Essa força possui uma componente horizontal e uma componente vertical .
Vamos adotar como a direção do movimento e esboçar um diagrama para visualizarmos melhor o que está acontecendo:
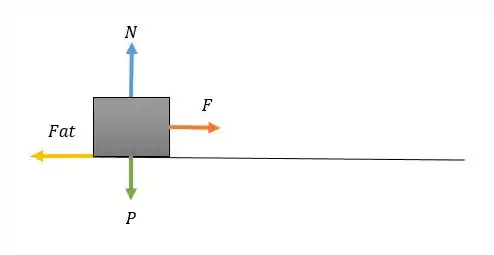
Então, nós temos que aplicar a 2º Lei de Newton para a caixa e calcular as forças normais e de atrito, para obter o coeficiente de atrito cinético através da razão . Vamos lá!
Passo 2
No eixo , temos a ação da força normal , da força peso para baixo e da componente também para baixo. Somando essas forças através da segunda lei de Newton, vamos ter:
E substituindo os valores do enunciado:
Passo 3
Agora vamos aplicar a segunda lei de Newton para o movimento na horizontal. Observe que agora nós temos uma aceleração, então nossa equação vai ficar:
Onde representa a força de atrito cinético que é contrária ao movimento. Isolando , vamos ter:
Agora considerando a massa e substituindo os valores do enunciado, encontramos:
Passo 4
Então, utilizando a fórmula do atrito cinético:
Vamos obter o coeficiente de atrito cinético na forma:
Portanto, a força normal é maior que o peso da caixa, devido ao componente descendente da força que empurra a caixa.
Valeu, galera! Até a próxima! 😉