Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.Problemas Adicionais - Ex. 62

Caixas são transportadas de um local para outro de um armazém por meio de uma esteira que se move com uma velocidade constante de . Em um certo local, a esteira se move ao longo de uma rampa que faz um ângulo de para cima com a horizontal, na horizontal e, finalmente, ao longo de uma rampa que faz um ângulo de para baixo com a horizontal. Suponha que uma caixa de é transportada pela esteira sem escorregar. Com que taxa a força da esteira sobre a caixa realiza trabalho quando a caixa se move (a) na rampa de para cima, (b) horizontalmente e (c) na rampa de para baixo?

Passo 1

Vamos iniciar esta questão fazendo um DCL para uma caixa na rampa:

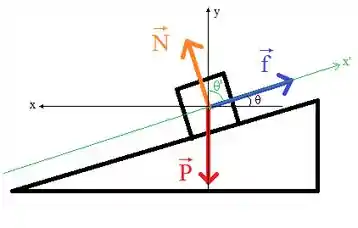
Devemos perceber que o enunciado nos diz que o corpo está se movendo com velocidade constante, portanto, nós temos um equilíbrio de forças. Além disso, devemos perceber que a força exercida pela esteira sobre a caixa é a combinação da força normal e da força de atrito. Portanto, aplicando a segunda lei de Newton:

Assim, sabemos que:

Portanto, o módulo da força que a esteira exerce sobre a caixa é igual ao módulo do peso.

Passo 2

Para determinar com que taxa a força da esteira sobre a caixa realiza trabalho quando a caixa se move na rampa de para cima, devemos lembrar que a taxa do trabalho nada mais é que a potência instantânea, que pode ser calculcado por:

Lembrando que já calculamos o , a velocidade foi dada e o entre a força e a velocidade será o explicitado na ilustração do DCL, então:

Passo 3

Quando a caixa está na horizontal, teremos somente agindo sobre o peso e a normal que agem perpendicular ao movimento, portanto o cosseno do ângulo entre o vetor da força que a esteira exerce na caixa e o vetor velocidade é nulo. Assim:

Passo 4

Para calculcar para a caixa descendo, podemos usar o mesmo DCL do início, considerando que o deslocamento está para baixo. Portanto, o ângulo entre a o vetor da força que a esteira exerce sobre a caixa pode ser calculado por:

Assim, usando a :

Resposta

;
;
.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois blocos estão ligados por um fio muito leve que passa por uma polia sem massa e sem atrito. (Figura 6.30 .) Deslocando-se com velocidade escalar constante, o bloco de 20,0N se move 75,0c m da esqu

Um trabalhador de uma fábrica exerce uma força horizontal para empurrar por uma distância de 4,5m um engradado de 30,0k g ao longo de um piso plano. O coeficiente de atrito cinético entre o engradado

Suponha que o trabalhador do Exercício 6.3 empurre o engradado para baixo de um plano inclinado de 30 ° abaixo da horizontal. a) Qual é o módulo da força aplicada pelo trabalhador para que o engradado

Utilize o Princípio dos trabalhos Virtuais enunciado na Seç. 7.3 para obter as condições de equilíbrio da alavanca[ Fig . a)] e do plano inclinado [Fig. b)]. Para isto, imagine que um pequeno deslocam

Um corpo de massa m= 300g , enfiado num aro circular de raio R= 1m situado num plano vertical, está preso por uma mola de constante elástica k = 200 N/m ao ponto C, no topo do aro (Fig.). Na posição r