Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.1 - Ex. 7
Dois blocos estão ligados por um fio muito leve que passa por uma polia sem massa e sem atrito. (Figura .) Deslocando-se com velocidade escalar constante, o bloco de se move da esquerda para a direita e o bloco de move-se de cima para baixo. Nesse processo, quanto trabalho é realizado:
a) sobre o bloco de
i) pela gravidade; e
ii) pela tensão no fio?
b) Sobre o bloco de
i) pela gravidade;
ii) pela tensão no fio;
iii) pelo atrito; e
iv) pela força normal?
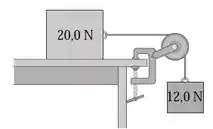c) Calcule o trabalho total realizado sobre cada bloco.
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá o seguinte esqueminha:
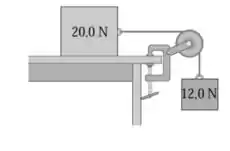
Os blocos se movimentam com velocidade constante, isso quer dizer que as forças estão em equilíbrio. Olhando para o bloco de temos duas forças: a tensão e o peso, e eles devem ter o mesmo módulo e sentido contrário.
O trabalho realizado por uma força qualquer é onde é o ângulo formado entre a força e o deslocamento. Vamos ao que se pede!
- Já sabemos que e o peso do bloco menor é . O deslocamento foi de de cima para baixo, então o peso está no mesmo sentido do deslocamento e a tensão no sentido contrário. Sabendo disso podemos calcular os trabalhos.
- Para a força peso. O deslocamento é no mesmo sentido da força peso, então o ângulo entre eles é . O trabalho da força peso vai ser:
- Para a força tensora. O deslocamento é no sentido oposto, então . O trabalho da força tensora vai ser:
- Lembrando que pra calcular o trabalho precisamos do ângulo da força com o deslocamento. A fórmula do trabalho é . Juntando isso com as informações do passo anterior, podemos calcular os trabalhos, saca só:
Passo 2
Agora para o bloco de . Ele tem forças: força peso (vertical para baixo) e normal (vertical para cima) e elas tem o mesmo módulo e sentidos contrários. E na horizontal temos a tensão (horizontal para direita) e o atrito (horizontal para a esquerda). Essas duas últimas também possuem módulos iguais e sentidos contrários, isso porque os blocos se movimentam com velocidade constante.
Sendo assim, na vertical temos que o peso é igual a normal:
E na horizontal também teremos o equilíbrio das forças:
Mas já sabemos quanto vale a força tensora! É o mesmo fio, então a força é igual! Assim:
E quanto aos deslocamentos? Bom, como o sistema se move junto, enquanto o bloco menor de move para baixo, o bloco maior também se desloca , mas para a direita. O bloco maior não se move na vertical, apenas na horizontal.
Com todas essas considerações, podemos então calcular os trabalhos.
Passo 3
- Da gravidade. O deslocamento é horizontal e a gravidade é na vertical, então (spoiler: quando a força não for na direção do deslocamento, ela não realiza trabalho!).
- Da força tensora. A força tensora é no mesmo sentido do deslocamento, então o ângulo entre eles é . O trabalho então vai ser:
- Da força de atrito. Essa força é SEMPRE contrária ao movimento, então o ângulo dela com o deslocamento forma . Colocando na fórmula:
- Da força normal. A força normal é perpendicular à superfície de contato, e nesse caso é vertical para cima (isso muda quanto temos um plano inclinado, por exemplo). O deslocamento é na horizontal, então o ângulo formado entre eles é . Sendo assim a força normal não realiza trabalho:
Colocando na fórmula:
A força peso não contribui diretamente para o deslocamento do sistema, então ela não realiza trabalho!
Passo 2
O trabalho total sobre cada bloco. O trabalho total é a soma de todos os trabalhos individuais. Outro spoiler: como o sistema se movimenta com velocidade constante podemos fazer a seguinte associação:
Sempre viu! Sempre que um sistema estiver em equilíbrio de forças, o trabalho total sobre ele deve ser nulo! Mas como na física a gente mostra fazendo a conta, vamos lá!
Para o bloco menor:
Agora para o bloco maior:
Assim o trabalho total é nulo.
Ufaaa, acabou!