Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 59
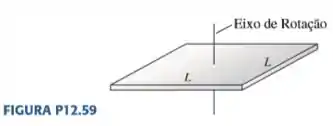
Calcule o momento de inércia de uma chapa retangular para rotações em torno de um eixo perpendicular à chapa e que passa por seu centro.
Passo 1
Vamos começar esse problema usando a equação de momento de inercia:
Se a gente colocar a origem do nosso sistema de coordenadas no centro da chapa, exatamente onde passa o eixo, na integral passa a ser:
Então se pegarmos um ponto qualquer da chapa, a posição dele vai ser o valor de uma hipotenusa formada pelas coordenadas e desse ponto, o que faz sentido.
Passo 2
Agora precisamos escrever em termos das coordenadas e , ou seja, cada ponto da chapa corresponde a um valor , nossa expressão fica:
Onde é a densidade superficial da chapa.
Essa densidade é a quantidade de massa por unidade de área:
E nosso fica:
Passo 3
Agora a gente substitui na nossa integral:
E o que fica faltando é determinar os limites de integração, como e são a distância do eixo até cada ponto da chapa e esse eixo passa no centro, basta a gente fazer:
Integrando:
E de novo em , ficamos com:
Como nesse caso a área é já que a chapa é quadrada:
Simplificando: