Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 4
Calcule o momento de inércia de um cubo homogêneo de massa e aresta , em relação a um diâmetro (eixo que passa pelos centros de duas faces opostas).
Passo 1
Primeiro vamos fazer uma ilustração, olha só:
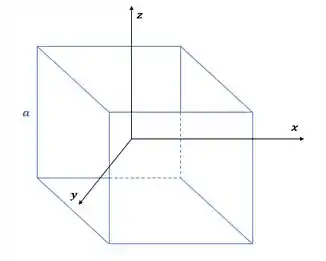
Para resolver essa questão vamos lembrar da teorema dos eixo perpendiculares. Como o cubo é simétrico, então . Logo,
Isto é,
Como colocamos em relação ao eixo z, esse é o momento de inércia que queremos achar.
Passo 2
Agora vamos ver como fica o . Temos que:
Onde e .
Vamos integrar do ponto da origem do eixo até a borda e multiplicamos por dois, pois tem o outro lado do cubo 😉.
Logo,
Assim,
Mas do passo 1, sabemos o seguinte:
Resposta
Exercícios de Livros Relacionados
Um disco uniforme possui raio R0 e massa M0. Seu momento de inércia para um eixo perpendicular ao plano do disco no centro do disco é 1 / 2M 0 R 0 2 . Você deverá dividir o momento de inércia do disco
Uma nova espécie de enguia foi descoberta, com a mesma massa, porém com um quarto do comprimento e o dobro do diâmetro da enguia americana. Qual é a relação entre seu momento de inércia em torno de se
Determine o momento de inércia de um cone maciço uniforme em relação a um eixo que passa através de seu centro (Figura P9.90). O cone possui massa M e altura h. O raio do círculo de sua base é igual a
Um ônibus de passageiro em Zurique, na Suíça, usa sua potência motora oriunda da energia acumulada em um volante grande. Utilizando-se de energia da rede elétrica, a roda é colocada em movimento perio
Um disco uniforme fino possui massa M e raio R. Fazemos um buraco circular de raio R/4 centralizado em um ponto situado a uma distância R/2 do centro do disco.a) Calcule o momento de inércia do disco