Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 10.Problemas - Ex. 10
Duas partículas de massas e são soltas em repouso, separadas de uma distancia inicial , movendo-se apenas sob o efeito de sua atração gravitacional mútua. Calcule as velocidades das duas partículas quando se aproximam até uma distância uma da outra.
Passo 1
Nessa aí a gente vai ter que fazer uma conservaçãozinha de energia clássica. Dá uma olhada na situação aí embaixo.
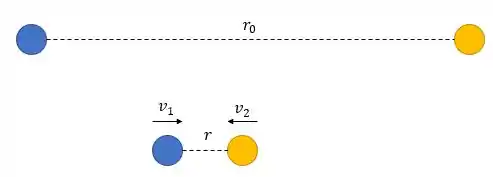
Primeiro as partículas estão separadas de uma distância . Conforme elas vão se atraindo, vão adquirindo velocidade até chegar na menor distância possível .
Passo 2
Então vamos conservar energia entre uma situação e outra.
Outra coisa que a gente pode fazer é conservar a quantidade de movimento pras duas situações. Primeiro, as esferas estavam paradas , e depois, cada uma delas vai ter a velocidade indicada na figura.
Então vamos substituir lá em cima!
Vamos dividir tudo por .
Fazendo o m.m.c. e dando uma arrumada, vamos obter:
Passo 3
Agora que achamos , é só jogar na equação da quantidade de movimento que temos ali em cima!