Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.1 - Ex. 6

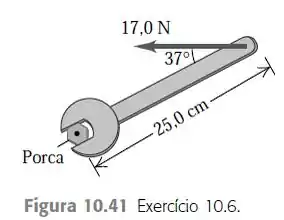
Um operário está usando uma chave de boca para afrouxar uma porca. A ferramenta tem 25,0 cm de comprimento, e ele exerce uma força de 17,0 N sobre a extremidade do cabo formando um ângulo de 37 ° com o cabo (Figura 10.41). a) Qual torque o operário exerce sobre o centro da porca? b) Qual é o torque máximo que ele pode exercer com essa força, e como a força deve ser orientada?

Passo 1

Eaee, belezinha?? Bom... um operário, a fim de afrouxar uma porca, aplica uma força de 17   N em uma chave de boca de 25   c m de tal forma que temos a seguinte figura:

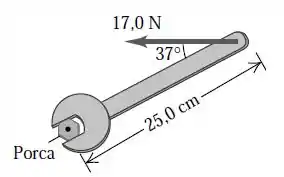
Queremos calcular o torque exercido pelo funcionário e o torque máximo que ele pode exercer com essa força... e como a força deve ser orientada.

Para isso, sabemos que a magnitude do torque τ é dado pelo produto entre a força F e o braço de alavanca l :

τ = F ⋅ l

Com l = r sen ⁡ θ .

Passo 2

  1. Temos que: r = 0,250 m φ = 37 °

    2. Então:

    τ = 17 N ⋅ 0,250 m ⋅ sen ⁡ 37 ° ∴

    τ = 2,56 N ⋅ m

    O torque é no sentido anti-horário.

    Passo 3

  2. O torque é máximo quando φ = 90 ° e a força é perpendicular à chave inglesa.

Assim, o torque máximo é:

τ m á x i m o = 17 N ⋅ 0,250 m ⋅ sen ⁡ 90 ° ∴

τ m á x i m o = 4,25 N ⋅ m

Se a força é direcionada ao longo da alavanca, o torque é zero.

O torque aumenta à medida que o ângulo entre a força e o punho aumenta.

Resposta

  1. τ = 2,56 N ⋅ m o sentido anti-horário.
  2. τ m á x i m o = 4,25 N ⋅ m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco uniforme de 120 k g , com raio igual a 1,4 m , gira inicialmente com uma rapidez angular de 1100 r e v / m i n . Uma força tangencial constante é aplicada a uma distância radial de 0,60 m do
No sistema descrito no problema 120, as constantes de força valem 60 N / m . O sistema parte do repouso e acelera lentamente até que as massas estejam a 0,80 m do centro do cilindro. Qual foi o trabal
A figura mostra um cilindro maciço de massa M e raio R , ao qual foi preso um segundo cilindro maciço, de massa m e raio r . Um cordão é enrolado em torno do cilindro menor. O cilindro maior está sobr
Um bastão uniforme tem comprimento L e massa M e pode girar livremente em torno de um eixo horizontal em uma de suas extremidades, como mostrado na figura. O bastão é largado do repouso em θ = θ 0 . M
Calcule o torque, em relação à origem, da força gravitacional F → = - m g j ^ que atua sobre uma partícula de massa m localizada em r → = x i ^ + y j ^ , e mostre que este torque é independente da coo