Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 17.Exercícios e Problemas - Ex. 16
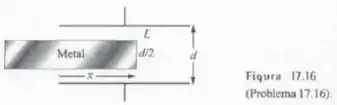
Calcule a variação da força sobre o bloco metálico da Figura 17.16 com a coordenada , sabendo-se que o capacitor tem uma carga fixa .
Passo 1
No exercício 15 nós achamos que a capacitância desse sistema é dada, em função de , por
Como a carga do capacitor é fixa, podemos escrever a energia potencial por
A força que atua sobre o metal será dada por
Usando a regra da cadeia:
Passo 2
Mas observe que
Assim,
Derivando a capacitância:
Assim,
Portanto,
Resposta
Exercícios de Livros Relacionados
Capacitância da terra. (a) Discuta como o conceito de capacitância também pode ser aplicado a um único condutor. (Dica: Na relação C = Q / V a b , considere um segundo condutor situado no infinito). (
O cilindro interno de um capacitor cilíndrico longo possui um raio r a e uma densidade linear + λ . Ele é circundado por um condutor cilíndrico co-axial com raio interno r b e densidade de carga linea
Capacitância Terra-Ionosfera. A Terra pode ser considerada um capacitor de condutor único (Veja problema 24.67). Ela também pode ser considerada em combinação a uma camada carregada da atmosfera, a io
Suponha que a bateria do problema 24.50 permaneça ligada enquanto você afasta as placas. Quais seriam as respostas dos itens (a), (b), (c) e (d) depois do afastamento das placas?
Considere um capacitor cilíndrico como o indicado na Figura 24.6. Seja d = r b - r a a distancia entre o condutor interno e o condutor externo. (a)Suponha que os raios dos condutores sejam ligeirament