Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 55
Considere um capacitor cilíndrico como o indicado na Figura 24.6. Seja a distancia entre o condutor interno e o condutor externo. (a)Suponha que os raios dos condutores sejam ligeiramente diferentes, de modo que . Mostre que o exemplo obtido no exemplo 24.4 (seção 24.1) para a cpacitancia do capacitor cilindro se rezu ao indicado na equação (24.2) – a equação para o capacitor com placas pararelas -, Em que A é a área da superfície de cada cilindro. Use a aproximação para . (b)Embora a Terra seja esférica, sua superfície parece placa porque seu raio é muito grande. Use essa idéia para explicar como o resultado da parte (a) faz sentido do ponto de vista puramente geométrico.
Passo 1
Okaay!! Here we go! O exemplo 24.4 nos mostra que
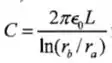
Para um capacitor cilíndrico. quando o x é bem pequeno. Logo, a área de cada condutor é aproximadamente
Passo 2
Temos que para (a):
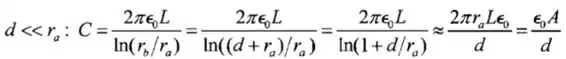
Passo 3
Usando o principio para responder (b), temos que para uma escala dessa forma, algo cilíndrico ou até mesmo esférico, pode ser comaprado com algo plano por ser muuuito grande.