17. Uma campânula cilíndrica de aço, sem fundo, de de altura, é baixada na água, a partir da superfície, até que seu teto fique a de profundidade. Que fração do volume da campânula será invadida pela água?
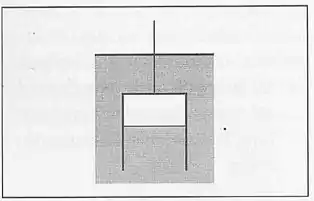
Passo 1
Bora lá pra mais um probleminha de hidrostática nesse maravilhoso e complicado livro de Física.
Após a campânula ser mergulhada na água, a pressão na interface água/ar devido à coluna de água é dada por:
Onde representa a altura da coluna de água dentro da campânula. Devido a essa altura, a pressão do ar dentro da campânula deixa de ser .
Passo 2
Agorao olha só o raciocínio que o nos força a ter. Sabemos que houve alteração de pressão e volume... Entretanto a questão falou alguma coisa sobre temperatura?
Viu só, se não falou, temos que pensar no que é melhor para nós. E o melhor é que consideremos que o ar passe por um processo isotérmico... Assim, aplicando a lei de obtemos que:
Onde representa a área da seção transversal da campânula... Assim, antes de ser mergulhada na água, a altura da coluna de ar é de e seu volume inicial é . Após ser mergulhada, a altura da coluna de ar é e seu volume final é . Como a pressão devido a coluna de ar deve ser igual a pressão devido à coluna de água na interface água/ar dentro da campânula, temos então que:
Vamos então tratar de simplificar a igualdade abaixo:
Muito bem! Vamos calcular agora, o valor de sabendo que:
Passo 3
Chegamos assim na seguinte equação:
Cujas raízes, dado o formato de equação , são dadas por:
Temos que pegar o valor que é menor do que , ou seja .
Isto representa uma fração de: