Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 1.Problemas - Ex. 16

16. Duas bolas de mesmo raio, igual a 10   c m , estão presas uma à outra por um fio curto de massa desprezível. A de cima, de cortiça, flutua sobre uma camada de óleo, de densidade 0,92   g / c m 3 com a metade do volume submersa. A de baixo, 6 vezes mais densa que a cortiça, está imersa metade no óleo e metade na água. (a) Ache a densidade ρ da cortiça; (b) Ache a tensão T no fio.

Passo 1

a) Bora lá pra mais um probleminha de hidrostática nesse maravilhoso e complicado livro de Física.

Bom! A primeira coisa que temos de fazer, é o diagrama de corpo livre para as duas esferas:

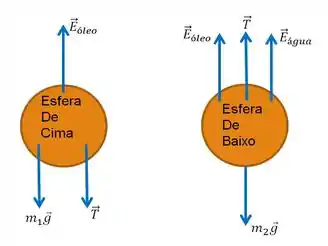
As forças agindo sobre a esfera superior são o peso (vertical para baixo), a tração (vertical para baixo) e o empuxo (pelo óleo, vertical para cima)... Portanto, temos que para o primeiro corpo vale a igualdade:

E ó l e o = m 1 g + T

Já para a esfera inferior, as forças agindo são a força peso (vertical para baixo), a tração (vertical para cima) e o empuxo devido ao óleo e a água (ambos verticais para cima):

E ó l e o + E á g u a + T = m 2 g

Onde ρ d representa a densidade do densímetro, V   seu volume total e ρ a   representa a densidade da água. Após ser mergulhado em outro líquido de densidade p , o densímetro se eleva a uma altura h   em relação a marca " 1 " , e o volume submerso passa a ser V s = V 0 - A h . Igualando o empuxo ao peso, obtemos que:

ρ V 0 - A h g = m g

Só que anteriormente, obtemos que:

m g = ρ d V g = ρ a V 0 g

O que nos leva à seguinte identidade:

ρ d V g = ρ a V 0 g =   ρ V 0 - A h g

ρ a V 0 g =   ρ V 0 - A h g

ρ a V 0 =   ρ V 0 - A h

Que maravilha! Chegamos a relação que queríamos, pois afinal de contas a densidade relativa entre o líquido e a água nada mais é do que a razão ρ / ρ a :

ρ ρ a = V 0 V 0 - A h

Pronto! Tá na mão a resposta!

Passo 2

A massa da esfera superior pode ser escrita como m 1 = ρ V , e a da esfera superior, que é seis vezes mais densa pode ser escrita como m 2 = 6 ρ V . Deste modo, podemos escrever o seguinte sistema:

ρ ó l e o V 2 g = ρ V g + T     ( I ) ρ ó l e o V 2 g + T + ρ á g u a V 2 g = 6 ρ V g     ( I I )

ρ ó l e o V 2 g - T = ρ V g     ( I ) ρ ó l e o V 2 g + T + ρ á g u a V 2 g = 6 ρ V g     ( I I )

Somando ( I ) e ( I I ) podemos então, retirar a tração T :

ρ ó l e o V g + ρ á g u a V 2 g = 7 ρ V g

2 ρ ó l e o V g + ρ á g u a V g = 14 ρ V g

2 ρ ó l e o + ρ á g u a = 14 ρ

ρ = 2 ρ ó l e o + ρ á g u a 14

Agora, é só substituir os valores numéricos correspondentes:

ρ = 2 ρ ó l e o + ρ á g u a 14

ρ = 2 ⋅ 0,92 + 1 14 g / c m 3

ρ ≅ 0,2 g c m 3 = 200   k g / m 3

Vamos passar para o k g / m 3 só para ficar no SI e podermos usar sem problemas na letra b, ok?

Passo 3

b) Neste item; para encontrar o valor de T , vamos pegar a equação ( I ) do P a s s o   2 :

ρ ó l e o V 2 g = ρ V g + T    

E em seguida, substituir os valores numéricos de cada variável conhecida, onde ρ ó l e o = 920   k g / m 3 :

T = ρ ó l e o V 2 g - ρ V g

T = V ρ ó l e o 2 g - ρ g

T = 4 3 π r 3 ρ ó l e o 2 g - ρ g

T = 4 3 π 0,1 3 920 2 ⋅ 9,81 - 200 ⋅ 9,81   N

T ≅ 10,7   N

Resposta

a)

ρ ≅ 0,2   g / c m 3

b)

T ≅ 10,7   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Há quem diga que poderíamos explorar Marte usando balões de gás para sobrevoar a superfície de perto. A força de empuxo da atmosfera manteria os balões no alto. A densidade da atmosfera marciana [e 0,
Uma barca aberta possui as dimensões indicadas na Figura 14.38. Sabendo-se que todas as partes da barca são feitas com placas de aço de espessura igual a 4,0 cm, qual é a massa de carvão que a barca p
As densidades do ar, do hélio e do hidrogênio (para p=1,0 atm e T=293 K) são 1,20 k g / m 3 , 0,166 k g / m 3 e 0,0899 k g / m 3 , respectivamente). a) Qual é o volume em metros cúbicos deslocado por
A propaganda de um certo carro afirma que ele flutua na água. a) Sabendo-se que a massa do carro é igual a 900 kg e seu volume interno é de 3 , om 3 , qual é a fração do carro que fica submersa quando
Um objeto com altura h , massa M e a área da seção reta Af l u t u a verticalmente em um liquido com densidade ρ . a) Calculde a distancia vertical entre a superfície do liquido e a parte inferior do