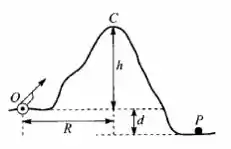
Um canhão lança um projétil por cima de uma montanha russa de altura h, de forma a passar quase tangenciando o cume C no ponto mais alto da sua trajetória. A distância horizontal entre o canhão e o cume é R. Atrás da montanha há uma depressão de profundidade d (Fig. 3.36). Determine a distância horizontal entre o ponto de lançamento O e o ponto P onde o projétil atinge o solo, em função de R, d e h.

Falaaa meus jovens, aqui o interessante é calcular o tempo que o projétil leva para subir e descer, assim a gente só joga na velocidade horizontal e matamos a questão. Vem comigo!

Para o cume C temos

Para saber vamos tirar da manga outra equação, saca só

Para o movimento da descida é quase a mesma coisa, só que mais fácil haha, vê só