Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 38

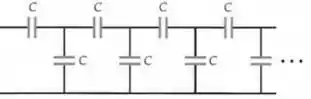
Qual é a capacitância equivalente (em termos de C , que é a capacitância de um dos capacitores) da escada infinita de capacitores mostrada na Figura 24-39?

Passo 1

Cara... Anota uma coisa aí! Toda vez que você tiver que resolver um circuito infinito, você vai pegar os primeiros (no caso os dois primeiros capacitores) e o restante, você vai substituir por C e q ...

POW! Repare então que podemos encontrar a capacitância total desse circuito fazendo...

C t o t = C C + C e q C + C + C e q

Onde C t o t é a simplificação da simplificação, ou seja...

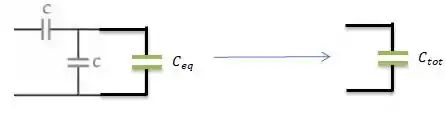
Passo 2

Mas olha que interessante... O circuito é infinito! Isso significa que C t o t é igual ao C e q , afinal no infinito não importa muito, neh? Então...

C t o t = C C + C t o t C + C + C t o t     →

Então agora basta isolar...

C t o t = C 2 + C C t o t 2 C + C t o t     →

C t o t 2 C + C t o t = C 2 + C C t o t     →

2 C C t o t + C t o t 2 = C 2 + C C t o t     →

Passando tudo para um lado só...

2 C C t o t + C t o t 2 - C 2 - C C t o t = 0   →

C t o t 2 + C C t o t - C 2 = 0   →

Repare que isso aí é uma equação do segundo grau, ou seja...

C t o t = - C ± C 2 - 4 - C 2 2   →

C t o t = - C ± 5 C 2 2   →

C t o t = - C ± C 5 2   →

Como não faz sentido capacitância negativa...

C t o t = - C + C 5 2   →

C t o t = C 5 - 1 2  

Resposta

C t o t = C 5 - 1 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um teclado de computador, cada tecla contém uma pequena placa metálica que funciona como uma das placas metálicas de um capacitor com ar. Quando pressionamos a tecla, a distância entre as placas di
O capacitor com placas pararelas imerso no ar indicado na figura 24.40 possui duas placas condutoras de área A . A placa inferior repousa sobre um suporte fixo e a placa superiore está suspensa por qu
Um capacitor com placas paralelas possui o volume entre as placas preenchido com uma plástico cuja constante dielétrica é K . O módulo da carga de cada placa é igual a Q . Cada carga possui área A e a
Na figura, uma diferença de potencial V = 100 V é aplicada a um circuito de capacitores cujas capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Determine (a) q 3 ; (b) V 3 ; (c) a energi
Um capacitor de placas paralelas é conectado a uma bateria. O espaço entre as placas está vazio. Se a separação entre as placas é triplicada enquanto o capacitor permanece conectado à betaria, qual é