Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Exercício - Ex. 16
16. Repita o Exercício com um circuito constituído somente pelo resistor e pelo capacitor em série. Para o item , determine as amplitudes das tensões através do resistor e através do capacitor.
Passo 1
A grande sacada dessa questão é que embora o enunciado diz que você dispõe de um resistor, um indutor e um capacitor o circuito que será ligado irá contar apenas com o resistor e com o capacitor.
A partir daí vamos usar algumas equações que vimos até agora no livro de acordo com esse circuito.
Passo 2
O enunciado pede impedância do circuito que está ligando o resistor e o capacitor, nesse caso a impedância é dada por:
O enunciado nos dá o mas não , então vamos ter que conseguir igualzinho como conseguíamos na seção anterior:
Ou seja:
Passo 3
A equação nos diz que:
O enunciado nos deu e nós achamos no item anterior, então:
Passo 4
O enunciado dessa questão nos pede as amplitudes das tensões enquanto o do Exercício pedia “as amplitudes das voltagens”. E aí? Bom, é a mesma coisa. Se tiver alguma dúvida volte na página do livro, tá bom?
A equação nos diz que:
E a equação diz que:
Agora o que nos resta é substituir o valor de que o enunciado nos dá e os valores de e que descobrimos nos passos e , respectivamente. Ou seja:
Passo 5
Como o exercício pede em relação a corrente sabemos que é a corrente que achamos do circuito resistor e capacitor, então (de acordo com a equação ):
Em graus o resultado seria:
Passo 6
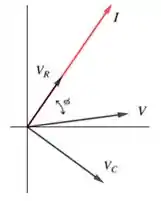
Agora é só fazer o diagrama de fasores e é isso galerinha!
Resposta
