Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas desafioadores - Ex. 90
Um capacitor de alarme contra roubo. A capacitância de um capacitor pode ser alterada por um material dielétrico que, embora fora do capacitor, esteja suficientemente próximo do capacitor para ser polarizado pelo campo elétrico existente nas bordas de um capacitor carregado. Esse efeito é da ordem picofarads (), porém ele pode ser usado por um circuito eletrônico apropriado para detectar uma variação do material dielétrico que está nas vizinhanças do capacitor. Tal material dielétrico poderia ser o corpo humano, e esse efeito poderia ser usado para projetar uma alarme contra ladrões. Considere o circuito simples indicado na Figura 26.82. A fonte de tensão possui fem e o capacitor apresenta capacitância . O circuito eletrônico para detectar a corrente, representado por um amperímetro no diagrama, possui resistência desprezível, sendo capaz de detectar uma corrente da ordem de pelo menos e que persista por um tempo de pelo menos depois que a capacitância mudar repentinamente de para . O alarme contra ladrões é projetado para ser ativado quando a capacitância varia de 10%. (a)Determine a carga no capacitor de quando ele está plenamente carregado. (b)Supondo que o capacitor esteja plenamente carregado antes de o intruso ser detectado e desprezando o tempo necessário para produzir a variação de capacitância de 10%, de duza uma equação que forneça a corrente que passa em R em função do tempo desde o momento em que a capacitância foi alterada. (c) Determine o intervalo de valores para os quais a resistência R satisfaça as condições especificadas do alarme contra ladrões. O que acorreria se o valor de R fosse demasiadamente pequeno? E se fosse muito grande?
Passo 1
Quando muda depois que o capacitor é carregado, a tensão pelo capacitor muda. A corrente flui pelo resistor até a tensão no capacitor se igualar a fem.
(a)Totalmente carregado:
(b)A corrente inicial logo depois que o capacitor é carregado:
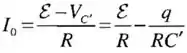
Isso nos dá que:
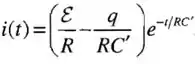
Onde,
Passo 2
(c)Nos precisamos de uma resistência tal que a corrente vai ser bem maior que para um tempo maior que . Isso requere em :
Isso nos dá que:
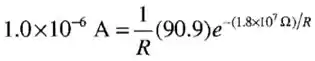
E,
Passo 3
Uma equação mó louca, mas resolvendo para , temos:
