Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Questões Conceituais - Ex. 13

Um capacitor de placas paralelas consiste de duas placas quadradas, de tamanho L ×   L , separadas pela distância d . As placas são carregadas com cargas ± Q . Qual será o valor da razão E f / E i entre a intensidade do campo elétrico final e a intensidade do campo elétrico inicial se (a) Q for dobrada, (b) L for dobrado e (c) d for dobrada? Em cada item, apenas uma grandeza sofre variação, as outras se mantêm em seus valores iniciais..

Passo 1

Fala aí galerinha, blz??

Vamos se atentar à figura abaixo...

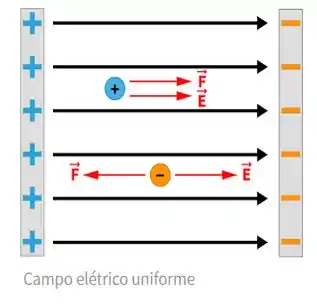
Como podemos ver, o campo elétrico dessa partícula em azul é dado pela contribuição do campo elétrico gerado pelas duas placas, tanto a positiva quanto a negativa...

Tomando essas placas como simples cargas ± Q , podemos então dizer que o campo elétrico resultante será dado por...

E R e s = E - + E +

E R e s = k 0 Q d 2 + k 0 Q d 2

E R e s = 2 k 0 Q d 2

Ou seja, não depende absolutamente nada do comprimento das placas... Pelo que já podemos garantir a resposta da letra (b)...

E f E i = 1

Passo 2

a)

Vamos ver então o que acontece quando a cargas Q é dobrada...

Antes, tínhamos que...

E i = 2 k 0 Q d 2

Com Q ' = 2 Q , ficamos com...

E f = 4 k 0 Q d 2

Aí é só fazer a relação...

E f E i = 4 k 0 Q d 2 2 k 0 Q d 2

E f E i = 2

Passo 3

c) E o mesmo vale pra essa última letra aqui... A diferença é que   d vai dobrar...

Antes...

E i = 2 k 0 Q d 2

E então, depois...

E f = 2 k 0 Q ( 2 d ) 2

E i = 1 2 k 0 Q d 2

Aí ficamos com a razão...

E f E i = 1 2

Pronto! Finalizamos aqui, guys!

Resposta

a)

E f E i = 2

b)

E f E i = 1

c)

E f E i = 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma carga positiva Q é distribuída uniformemente ao longo de uma semicircuferência de raio a (Figura 21.49). Obtenha o campo elétrico (Módulo, direção e sentido) no centro de curvatura P.
Um fio retilíneo carregado como aquele indicado na Figura 21.25 se estende desde y = 2,50c m até y = - 2,50c m . A carga total distribuída uniformemente sobre o fio é igual - 9,0n C . (a) Obtenha o ca
Uma carga positiva Q é distribuída uniformemente sobre o eixo O x de x = 0 até x = a . Uma carga puntiforme negativa - Q é distrubuída sobre o eixo O x de x = 0 até x = - a . (a) Uma carga puntiforme
(a)Seja f ( x ) uma função par de x de modo que f x = f - x . Mostre que ∫ - a a f ( x ) d x = 2 ∫ 0 a f ( x ) d x . (Sugestão: escreva a integral de - a até a como a soma da integral de - a até 0 com
Uma carga positiva Q é distribuída uniformemente sobre o eixo O x de x = 0 até x = a . Uma carga puntiforme positiva q . Está sobre a parte positiva do eixo O x , no ponto x = a + r , a uma distância