Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 93
Um capacitor tem placas retangulares de comprimento e largura . A placa superior está inclinada por um pequeno ângulo, como mostra a Figura. A separação entre as placas varia desde à esquerda, até à direita, onde é muito menor que e . Calcule a capacitância deste arranjo.
Passo 1
Fala galera, beleza?
Vamos usar a dica dada. Notemos que a gente tem vários capacitores ligados em paralelo. Assim,
onde
sendo a distância entre as placas.
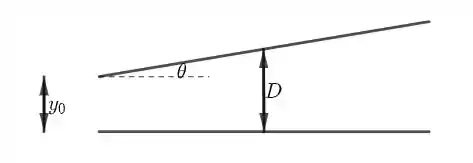
Temos que
Assim, segue que
Portanto,
Passo 2
Dessa forma, a capacitância final será
Resposta
Temos que .
Exercícios de Livros Relacionados
Uma balança de capacitância é mostrada na figura 24-50. A balança tem um peso preso em um lado e um capacitor com um espaçamento variável no outro lado. Considere que a placa superior do capacitor ten
Um capacitor de placas paralelas preenchido com ar tem espaçamento d e placas com área A . O capacitor é carregada a uma diferença de potencial V e, é então, removido da fonte de tensão. Uma lâmina di
Você trabalha em uma companhia de engenharia que produz capacitores usados para armazenamento de energia para lasers pulsados. Seu gerente pede à sua equipe para construir um capacitor de placas paral
Um capacitor retangular de placas paralelas tem comprimento a e largura b , e tem um dielétrico de largue b parcialmente inserido até uma distância x entre as placas, como mostra a Figura 24-89. (a) D