Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 97

Uma carga negativa - Q é distribuída uniformemente ao longo da quarta parte de uma circunferência de raio a , que está sobre o primeiro quadrante, com centro de curvatura a origem. Encontre os componentes x e y do campo elétrico na origem.

Passo 1

Lembrando que o campo é dado por:

E → = k q r 2 r ^ = k q a 2 r ^

Ele pode ser reescrito da forma diferencial dada por:

d E = k a 2 d Q

Representando a carga citada no enunciado através do esboço:

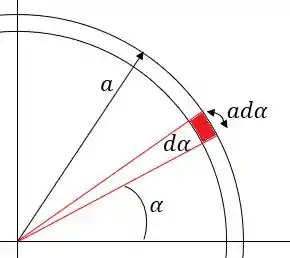
Precisamos lembrar que um quarto do comprimento de uma circunferência é dada, nesse caso, por:

2 π a 4 = π a 2

E como um elemento de carga diferencial é apenas uma parte de toda a carga distribuída, temos que a carga neste trecho pode ser escrita como:

d Q = a d α π a 2 Q = 2 π Q d α

Passo 2

Agora, desenhando uma representação de um elemento do campo elétrico e seus componentes:

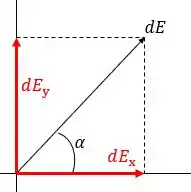
Esses componentes podem ser escritos através das relações trigonométricas do triângulo formado no desenho, tal que:

d E x = d E c o s α

E

d E y = d E s e n α

Passo 3

Agora, substituindo o valor de d E nessas equações conseguimos encontrar os resultados das componentes:

d E x = k a 2 d Q c o s α = k a 2 2 π Q d α c o s α

Reorganizando a equação:

d E x = 2 k a 2 π Q c o s α d α

E integrando ambos os lados da equação:

∫ d E x = ∫ 0 π / 2 2 k a 2 π Q c o s α d α

Podemos perceber que o intervalo de integração da angulação vai de 0 a π / 2 devido a ele representar o primeiro quadrante por onde a carga está distribuída. Logo:

E x = 2 k a 2 π Q ∫ 0 π / 2 c o s α d α

E x = 2 k a 2 π Q s e n α | π 2 0 = 2 k a 2 π Q s e n π 2 - s e n 0

Portanto:

E x = 2 k a 2 π Q

Da mesma forma, para a componente vertical:

E y = 2 k a 2 π Q ∫ 0 π / 2 s e n α d α

E y = 2 k a 2 π Q - c o s α | π 2 0 = 2 k a 2 π Q - cos ⁡ π 2 + cos ⁡ 0

Então:

E y = 2 k a 2 π Q

Resposta

E x = E y = 2 k a 2 π Q

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um anel de raio R = 2,40c m de raio contém uma distribuição uniforme de cargas e o módulo do campo elétrico E resultante é medido ao longo do eixo central do anel (perpendicular ao plano do anel). A q
A Fig. Abaixo mostra dois anéis concêntricos, de raios R e R' = 3,00R, que estão no mesmo plano. O ponto P está no eixo central z, a uma distância D = 2,00R do centro dos anéis. O anel menor possui um
A Fig. 22-43 mostra dois anéis não condutores paralelos, com o centro na mesma reta perpendicular aos planos dos anéis. O anel 1, de raio R , possui uma carga uniforme q 1 ; o anel 2, também de raio R
Na Fig. 22-46, uma barra não condutora de comprimento L = 8,15c m tem uma carga - q = - 4,23f C uniformemente distribuída. (a) Qual é a densidade linear de cargas da barra? Determine (b) o módulo e (c
Na Fig. 22-44, uma barra fina de vidro forma uma semicircunferência de raio r = 5,00c m . Uma carga + q = 4,50p C está distribuída uniformemente na parte superior da barra e uma carga - q = - 4,50p C