Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 59

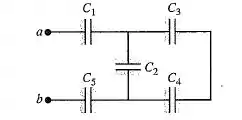
Na figura 24.32, C 1 = C 5 = 8,4   μ F e C 2 = C 3 = C 4 = 4,2   μ F . A diferença de potencial aplicada é V a b = 220   V . (a) Qual é a capacitância equivalente do circuito entre os pontos a e b? (b) Calcule a carga de cada capacitor e a diferença de potencial através de cada capacitor.

Passo 1

letra a)

Os capacitores C 3 e C 4 estão em série, logo:

1 C 34 = 1 C 3 + 1 C 4

1 C 34 = 1 4,2 ⋅ 10 - 6 + 1 4,2 ⋅ 10 - 6

1 C 34 = 2 4,2 ⋅ 10 - 6

C 34 = 2,1 ⋅ 10 - 6   F

Passo 2

Os capacitores C 2 e C 34 estão em paralelo, logo:

C 234 = C 2 + C 34

C 234 = 4 , 2 ⋅ 10 - 6   + 2,1 ⋅ 10 - 6  

C 234 = 6,3 ⋅ 10 - 6   F

Passo 3

Os capacitores C 234 , C 1 e C 5 estão em paralelo série, logo:

1 C e q = 1 C 234 + 1 C 1 + 1 C 5

1 C e q = 1 6,3 ⋅ 10 - 6   + 1 8,4 ⋅ 10 - 6   + 1 8,4 ⋅ 10 - 6  

1 C e q = 1 6,3 ⋅ 10 - 6   + 2 8,4 ⋅ 10 - 6  

1 C e q = 8,4 + 2 ⋅ 6,3 52,92 ⋅ 10 - 6  

1 C e q = 21 52,92 ⋅ 10 - 6  

C e q = 2,52 ⋅ 10 - 6   F

Passo 4

letra b)

Como os capacitores C 234 , C 1 e C 5 estão em série:

Q 234 = Q 1 = Q 5 = Q

V 1 + V 2 + V 5 = V a b

Passo 5

Como sabemos a capacitância equivalente à diferença de potencial entre os terminais, podemos achar a carga total do circuito.

Q = C e q V a b

Q = 2,52 ⋅ 10 - 6 ⋅ 220

Q = 550 ⋅ 10 - 6 C

Então:

Q 1 = 550 ⋅ 10 - 6 C

Q 5 = 550 ⋅ 10 - 6 C

Passo 6

Podemos achar agora os potenciais V 1 e V 5 :

Para V 1 :

V 1 = Q 1 C 1

V 1 = 550 ⋅ 10 - 6 8,4 ⋅ 10 - 6

V 1 = 65   V

Para V 5 :

V 5 = Q 5 C 5

V 5 = 550 ⋅ 10 - 6 8,4 ⋅ 10 - 6

V 5 = 65   V

Passo 7

Por estarem em série:

V 1 + V 2 + V 5 = V a b

V 2 = V a b - V 1 - V 5

V 2 = 220 - 65 - 65

V 2 = 90   V

Passo 8

Podemos achar agora a carga Q 2 :

Q 2 = C 2 V 2

Q 2 = 4,2 ⋅ 10 - 6 ⋅ 90

Q 2 = 378 ⋅ 10 - 6   C

Passo 9

Como vimos:

Q 234 = Q

E além disso:

Q 234 = Q 2 + Q 34 = Q

Mas como C 3 e C 4 estão em série, suas cargas são iguais Q 3 = Q 4 logo:

Q 2 + 2 Q 3 = Q

Q 3 = 1 2 ( Q - Q 2 )

Q 3 = 1 2 ( 550 ⋅ 10 - 6 - 378 ⋅ 10 - 6 )

Q 3 = 172 ⋅ 10 - 6   C

Logo:

Q 4 = 172 ⋅ 10 - 6   C

Passo 10

Podemos achar agora os potenciais V 3 e V 4 :

Para V 3 :

V 3 = Q 3 C 3

V 3 = 172 ⋅ 10 - 6 4,2 ⋅ 10 - 6

V 3 = 41   V

Para V 4 :

V 4 = Q 5 C 5

V 4 = 172 ⋅ 10 - 6 4,2 ⋅ 10 - 6

V 4 = 41   V

Resposta

letra a) C e q = 2,52 ⋅ 10 - 6   F

letra b)

Q 1 = 550 ⋅ 10 - 6 C , Q 2 = 378 ⋅ 10 - 6   C , Q 3 = 172 ⋅ 10 - 6   C , Q 4 = 172 ⋅ 10 - 6   C e Q 5 = 550 ⋅ 10 - 6 C

V 1 = 65   V , V 2 = 90   V , V 3 = 41   V , V 4 = 41   V e V 5 = 65   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O livre percurso médio das moléculas em um gás é l . Qual é a probabilidade de uma molécula ter um vôo livre de comprimento l ?
A vida média de um nêutron fora do núcleo atômico é 16 minutos. Qual é a probabilidade de um nêutron livre sobreviver uma hora?
Um frasco de perfume é aberto por um breve intervalo de tempo, liberando N moléculas no ar. Um minuto após serem liberadas, as moléculas de perfume apresentam uma dispersão dada por r r m s = 2,5c m .
A vida média de um núcleo radioativo é τ . Quanto vale t 2 - ?
Um bêbado anda em passeio aleatório, com passos de 70 c m , e o comprimento total de sua trajetória é 5,0 k m . Calcule o valor r r m s de sua posição final.