Uma carga positiva está fixa no ponto e e uma carga negativa está fixa no ponto e. a)Faça um diagrama para mostrar as posições das cargas. b)Deduza uma relação para o potencial em qualquer ponto sobre o eixo em função da coordenada. Considere zero o potencial a uma distância infinita das cargas. c)Para qual ponto do eixo o potencial? d)Faça um gráfico do potencial sobre o eixo em função de de até. e)Qual seria a resposta do item (b) quando? Explique como esse resultado é obtido.
Passo 1
letra a)
Como está fixa no ponto eestá fixa no ponto e, temos:
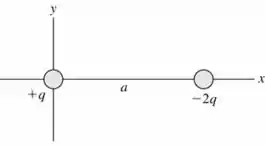
Passo 2
letra b)
Queremos o potencial em todos os pontos do eixo .
O potencial total em qualquer ponto é a soma algébrica dos potenciais das duas cargas.
Precisamos então olhar os três casos.
, e
Passo 3
Para :
Passo 4
Para :
Passo 5
Para :
Passo 6
De modo geral, podemos escrever:
Passo 7
letra c)
Queremos saber em quais pontos, .
Considerando os potenciais que encontramos no item anterior, o potencial será nulo, quando o numerador zerar. Logo:
Passo 8
letra d)
Fazendo um gráfico do potencial que encontramos, podemos ver que há 3 regiões onde o potencial não é nulo, assim como nós encontramos.
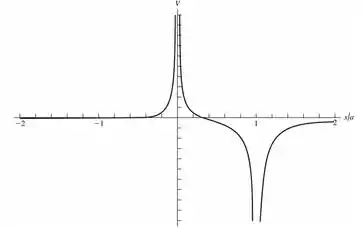
Passo 9
letra e)
Queremos saber o que acontece com o potencial:
quando .
Que é o potencial de uma carga .
Resposta
letra a)

letra b)
letra c)e
letra d)

letra e)