Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 23.Problemas - Ex. 60
Uma pequena esfera, com massa igual a 1,5 g, está pendurada por um fio isolante entre duas placas paralelas verticais, separadas por uma distância igual a 5 cm. As placas são isolantes e possuem densidades de carga superficial uniformes e . A carga da esfera é . Calcule a diferença de potencial entre as placas para que o fio fique inclinado a um ângulo de 30° em relação à vertical.
Passo 1
Há 3 forças atuando na esfera: peso, tração e elétrica.
Para resolvermos esse tipo de problema, precisamos usar a condição de equilíbrio:
Passo 2
Então precisamos decompor as forças
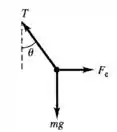
No eixo x temos:
No eixo y temos:
Dividindo uma equação pela a outra temos:
Passo 3
A força elétrica é:
Substituindo o campo elétrico temos:
Isolando o potencial:
Resposta
Exercícios de Livros Relacionados
53 . Uma partícula com carga + 7,60n C está em um campo elétrico uniforme, orientado da direita para a esquerda. Outra força além da elétrica atua sobre a partícula, de modo que ela se desloca para a
ANÁLISE DE MATERIAIS COM ÍONS. A espectrometria de retrodispersão de Rutherford (RBS, do inglês Rutherford backscattering spectrometry) é uma técnica utilizada para determinar a estrutura e a composiç
72 . ( a ) Supondo que uma gota de chuva, de raio igual a 0,650m m , possua carga igual a - 3,60p C uniformemente distribuída em seu volume, qual é o potencial elétrico sobre sua superfície? (Consider
54 . Cargas puntiformes idênticas, q = + 5,00μ C , são colocadas em ângulos opostos de um quadrado, cujo lado possui comprimento igual a 8,00c m . O ponto A está em um dos ângulosvazios e o ponto B es
O óvulo elétrico. Após a fecundação, os óvulos de muitas espécies passam por uma rápida mudança na diferença de potencial através de sua membrana externa. Essa alteração afeta odesenvolvimento fisioló