Um carro se desloca a 30 m/s saindo de um posto de gasolina enquanto sobe por uma pista inclinada em com o motor desligado. Até que altura ele subirá na rampa antes de começar a rolar de volta?
Passo 1
Bom galera, vamos esboçar a situação para compreendermos melhor o que esta acontecendo e representar o carro como uma partícula:
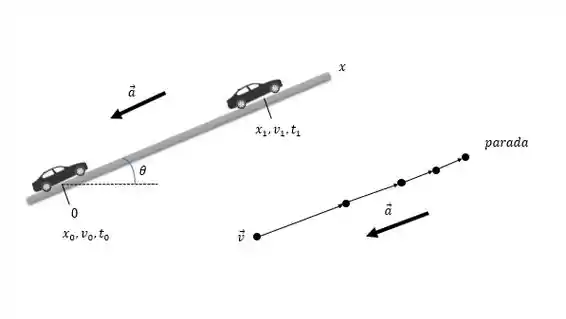
Nós conhecemos que: e precisamos encontrar .
Passo 2
Então, vamos lá:
Observe que o problema "termina" em um ponto de viragem, onde o carro tem uma velocidade instantânea de antes de voltar a descer. O movimento de reversão não faz parte desse problema. Se assumirmos que o carro rola sem atrito, então temos movimento em um plano inclinado sem atrito com uma desclassificação
A cinemática de aceleração constante fornece
Passo 3
Observe como os dois negativos foram cancelados para fornecer um valor positivo para .
Devemos incluir o sinal de menos porque o vetor aponta para baixo da inclinação, que está no negativo direção x.