Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 18
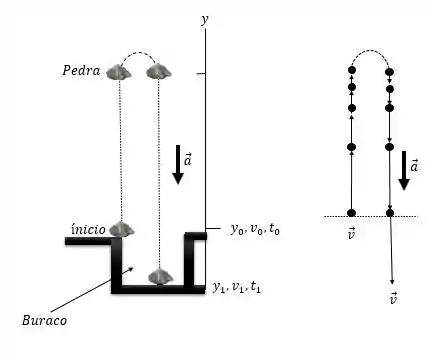
Uma pedra é atirada diretamente para cima com rapidez de 20 m/s. Ao retornar, ela cai em um buraco com 10 m de profundidade.
a. Qual é a velocidade da pedra no fundo do buraco?
b. Que distância ela percorreu no ar desde o instante em que foi liberada até bater no fundo do buraco?
Passo 1
Usaremos o modelo de partículas e as equações cinemáticas de aceleração constante.
Queremos encontrar: , e conhecemos , então bora calcular.
Passo 2
- Substituindo os valores conhecidos em , temos que:
- .
Uma das raízes desta equação é negativa e não é relevante fisicamente. A outra raiz é , que é a resposta para a parte (b).
Note que para encontrarmos a parte (a) foi preciso calcular primeiro a parte (b).
Passo 3
E então, utilizando a equação:
Vamos obter que:
E fechou, encontramos a parte (a).
Passo 4
O tempo de é um valor razoável. A velocidade da rocha ao atingir o fundo do buraco tem um valor negativo por causa de sua direção descendente. A magnitude de em comparação com , quando a rocha foi lançada acima, é consistente com o fato de que a rocha viaja uma distância adicional de 10 m no buraco.