Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 64
Enquanto a Terra gira em torno de si mesma, qual é a rapidez (a) de um estudante de física em Miami, Flórida, EUA, à latitude de 26° N e (b) de um estudante de física em Fairbanks, Alaska, à latitude de 65°N? Ignore a rotação da Terra em torno de Sol. O raio da Terra é de 6.400 km.
Passo 1
A latitude é θ, ou seja, a latitude vai indicar o ângulo, como podemos ver na figura abaixo
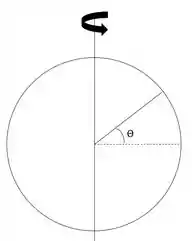
O raio da Terra é e
Outra coisa que devemos levar em conta, é que se o planeta é uma esfera, existe inúmeros círculos dentro dela, com raios diferentes, como podemos ver
Devido essas diferenças de raios, vamos usar
Passo 2
a. Em Miami tem o ângulo de . Assim, o raio é de, lembrando que , assim
A velocidade angular é
Então, a velocidade escalar é de
Passo 3
b. Em Fairbanks tem o ângulo de , então o raio é de
Como já temos a velocidade angular que é igual para qualquer parte da esfera, podemos substituir na velocidade escalar
Resposta
a.
b.