Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 14

Um carro viaja horizontalmente na direção leste-oeste com velocidade de 120   k m / h . O campo magnético local da Terra tem intensidade de 40   μ T e faz um ângulo de 45 ° com a horizontal. A componente horizontal do campo faz um ângulo de 17 ° com a direção norte-sul, desviando-se para o oeste. O carro tem uma antena vertical de comprimento igual a 1,00   m . Calcule a fem induzida na antena.

Passo 1

Fala pessoal, tudo tranquilo?

Assim como o último exercício, nesse problema vamos usar a discussão feita na seção 23.7 do livro!

A expressão que vamos utilizar nesse problema é dada na equação 23.37. A fem induzida gerada em um corpo carregado em movimento é

E m o v = ∫ v → × B → ⋅ d l →

A seguir faço um esboço da situação do problema:

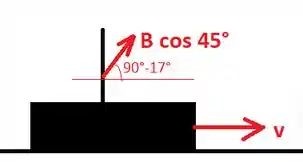
A componente do campo magnético no plano da imagem é

B cos ⁡ 45 °

Essa componente faz um ângulo de 17 ° com a vertical. Com isso, a fem induzida na antena será

E = v ⋅ B cos ⁡ 45 ° ⋅ s e n 90 ° - 17 ° ⋅ L

O termo s e n 90 ° - 17 ° aparece pelo produto vetorial. Com isso, temos

E = B v L cos ⁡ 45 °   s e n   73 °

Passo 2

Usando B = 40 ⋅ 10 - 6   T , L = 1,0   m e v = 120   k m / h = 33,3   m / s , temos que

E = 9 ⋅ 10 - 4   V

Essa é a fem entre os extremos da antena. Moral da história: é possível haver fem induzida mesmo que não haja fluxo magnético, basta haver um corpo condutor se movendo num campo magnético!

Resposta

E = 9 ⋅ 10 - 4   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) Mostre que os potenciais vetores A → = - B yi ^ e A → ' = B xj ^ geram o mesmo campo magnético.b) Determine a função escalar ψ tal que ∇ ψ = A → ' - A → .
Mostre que a corrente de deslocamento em um capacitor de placas paralelas pode ser expressa por I d = C d V d t
Um campo elétrico, no vácuo, é uniforme na região r5,00c m , e seu valor varia no tempo na forma E → = 2,00 k V m ms e n6238t / s . Para r5,00c m , o campo é nulo. Calcule a intensidade do campo magné
Considere o potencial vetor A → = B 2 - yi ^ + xj ^ a) Qual é o campo magnético associado a esse potencial?b) Mostre por cálculo direto que ∮ A → ⋅ d l → = ∫ S ∇ × A → ⋅ d S → , onde C é o círculo def
Considere a esfera de raio R , uniformemente carregada com a carga total Q , centrada no ponto r → = 0 → , e seja E → o campo elétrico gerado pela esfera. Mostre por cálculo direto que ∫ S E → ⋅ d S →