Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 26

A casa da moeda americana cunha, desde 1983, moedas de um centavo feitas de zinco com revestimento de cobre. A massa deste tipo de moeda é de 2,50 g. Use um modelo de cilindro homogêneo para a moeda, com altura 1,23 mm e raio 9,50 mm. Suponha que o revestimento de cobre seja uniformemente espesso em todas as superfícies. Se a massa específica do zinco é 7140 kg/m³ e a do cobre é 8930 kg/m³, qual a espessura do revestimento de cobre?

Passo 1

Bom, aqui nós podemos fazer um desenho do que está sendo dito pelo problema.

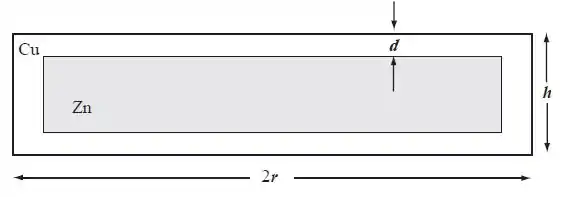
Nós queremos achar a espessura do cobre, d.

É isso ai, já sabemos o queremos, mas como achar d? Para isto precisamos perceber que a massa da moeda será:

m = m C u + m Z n

Lembrando da fórmula:

ρ = m V → m = ρ V

Substituindo:

m = ρ C u V C u + ρ Z n V Z n

Bom, a massa total e as massas específicas nós sabemos então precisamos somente dos volumes. A moeda se comporta como cilindro, portanto, o volume será

V = A b a s e . h

Como a base é um círculo:

V = π r ² . h

Para o zinco, a altura é ( h - 2 d ) e o raio ( r - d ). Então o volume:

V Z n = π r - d 2 . ( h - 2 d )

Para o cobre, vai ser um pouco mais complicado. Na parte superior e inferior da moeda o raio será r e d a altura. Mas também temos a lateral, e neste caso nós vamos usar o comprimento da circunferência ( 2 π r ) vezes a largura (d) e a altura (h-2d):

V C u = 2 π r ² d + 2 π r d h - 2 d

Substituindo na massa:

m = ρ C u [ 2 π r ² d + 2 π r d h - 2 d ] + ρ Z n π r - d 2 . ( h - 2 d )

Reorganizando:

m = ρ C u [ 2 π r ² d + 2 π r d h 1 - 2 d h ] + ρ Z n π r ² h 1 - d r 2 . ( 1 - 2 d h )

Passo 2

Bom, agora teremos que usar um artifício matemático e assumiremos que d ≪ h   e   d ≪ r , ou seja,

2 d h = 0   e   d r = 0  

Então:

m = d . ρ C u [ 2 π r ² + 2 π r h ] + ρ Z n π r ² h

Isolando d:

d = m - ρ Z n π r ² h 2 π r ρ C u r + h

Sabemos que:

ρ Z n = 7140   k g / m ³  

ρ C u = 8930   k g / m ³

m = 2,50   g = 2,50   x   10 - 3   k g

r = 9,50   m m = 9,50   x   10 - 3 m

h = 1,23   m m = 1,23   x   10 - 3 m

Substituímos:

d = ( 2,50   x   10 - 3   k g ) - π ( 7140   k g / m ³ ) ( 9,50   x   10 - 3 m ) ² ( 1,23   x   10 - 3 m ) 2 π ( 9,50   x   10 - 3 m ) ( 8930   k g / m ³ ) 9,50   x   10 - 3 m + 1,23   x   10 - 3 m

d = 1,7   μ m

Resposta

d = 1,7   μ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barca está em uma eclusa retangular de um rio de água doce. O comprimento da eclusa é 60,0 m e a largura é 20,0 m. As comportas de aço das duas extremidades estão fechadas. Uando a barca está flut
02. Milhas por quilograma. A densidade da gasolina é 737k g / m ³ ³. Se o seu novo carro híbrido faz 45,0 milhas por galão de gasolina, quantas milhas ele percorrerá por quilograma de gasolina? (Veja
03. Você compra uma peça retangular de metal com massa igual a 0,0158k g e dimensões de 5,0x15,0x30,0m m . O vendedor diz que o metal é ouro. Para verificar se é verdade, você deve calcular a densidad
04. Barra de ouro. Você ganha na loteria e decide impressionar seus amigos exibindo um cubo de ouro de um milhão de dólares. O ouro está sendo vendido a $426,60 por onça troy, e uma onça troy equivale
05. Duas esferas uniformes, uma de chumbo e outra de alumínio, possuem a mesma massa. Qual é a razão entre o raio da esfera de alumínio e o raio da esfera de chumbo?