Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 94

Uma casca cilíndrica fina e uma esfera maciça partem do repouso e descem rolando, sem deslizar, um plano inclinado de 3,0 m de comprimento. A casca cilíndrica atinge a base do plano 2,4 s depois da esfera. Determine o ângulo que o plano inclinado forma com a horizontal.

Passo 1

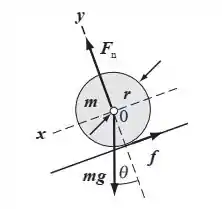
Aqui nessa questão temos dois objetos descendo um plano inclinado. Quando ainda não brincávamos com coisas rodando, a gente teria os dois chegando no pé do plano ao mesmo tempo, mas agora a gente tem que considerar que as coisas rodam e por isso translacionam mais devagar. Bora então dar uma olhada no movimento desses caras. Para os dois, teremos um diagrama de forças como esse:

Passo 2

Aplicando a segunda lei de Newton para um dos corpos:

∑ τ = f a t r = I α = I a r

f a t = I a r 2

No eixo paralelo ao plano:

∑ F = m g s e n θ - f a t = m a

m g s e n θ = m + I r 2 a

a = m g s e n θ m + I r 2  

Agora vamos substituir o momento de inércia para a casca e para a maciça:

a c = m g s e n θ m + 2 5 m r 2 r 2 → a c = 5 7 g s e n θ

a m = m g s e n θ m + m r 2 r 2 = 1 2 g s e n θ

Passo 3

Encontradas as acelerações, podemos pensar no movimento de descida do corpo:

Δ s = a t 2 2 → t = 2 Δ s a

t m - t c = Δ t

2 Δ s 1 2 g s e n θ - 2 Δ s 5 7 g s e n θ = Δ t

2 Δ s g s e n θ 2 - 7 5 = Δ t

s e n θ = 2 Δ s g Δ t 2 - 7 5

s e n θ = 2 Δ s g Δ t 2 - 7 5 2

θ = a r c s e n 2 Δ s g Δ t 2 - 7 5 2

θ = a r c s e n 2 × 3 9.81 × 2.4 2 - 7 5 2

Aqui é só pedindo ajuda pra calculadora mesmo!

θ = 0.058 °

Resposta

θ = 0.058 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jogador de boliche arremessa uma bola de raio R = 11 c m ao longo de uma pista. A bola (figura abaixo) desliza na pista com velocidade inicial v c m = 8,5 m / s e velocidade angular inicial ω 0 = 0
Um carretel é livre para girar em torno de um eixo fixo, e umm cordão enrolado em torno do eixo do carretel faz com que ele gire no sentido anti-horário (Figura 9-42a). No entanto, se o carretel é col
Largadas do repouso da mesma altura, uma casca esférica fina e uma esfera maciça, de mesma massa m e mesmo raio R , descem rolando um plano inclinado, sem deslizar, da mesma altura vertical H (figura
9.16P Suponha que a haste vista na Figura 9.20 não sinta nenhum atrito com a superfície de apoio e que sua queda inicie do repouso a partir da posição vertical. A) Em que ponto cai o centro de massa d