Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 99

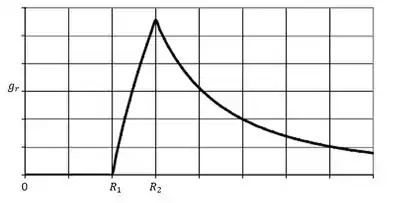
Uma casca esférica espessa, de massa M e massa específica uniforme, possui raio interno R 1 e um raio externo R 2 . Determine o campo gravitacional g , como função de r para 0 < r < ∞ . Esboce um gráfico de g , versus r .

Passo 1

Inicialmente, vamos dividir o campo três regiões: r < R 1 , R 1 < r < R 2 e r > R 2 .

Para r < R 1 :

Como estamos trabalhando com casca, a sua parte interna é oca. Portanto, como não há massa não há campo gravitacional.

g r < R 1 = 0

Passo 2

Para R 1 < r < R 2 :

Como estamos medindo o campo há uma distancia r do centro:

g = G m r 2

Agora precisamos achar a massa m que está dentro dessa região, mas antes vamos achar a densidade.

ρ = M V

Não esquece que entre o centro e a borda de esfera de raio R 1 é tudo oco. Logo,

V = 4 3 π R 1 3 - 4 3 π R 2 3 = 4 3 π ( R 1 3 - R 2 3 )

Portanto,

ρ = M 4 3 π ( R 1 3 - R 2 3 )

O volume entre o centro e a borda de esfera de raio r será:

V ' = 4 3 π r 3 - 4 3 π R 1 3 = 4 3 π ( r 3 - R 1 3 )

Assim,

m = ρ V ' = M 4 3 π ( R 1 3 - R 2 3 ) ⋅ 4 3 π r 3 - R 1 3 = M r 3 - R 1 3 R 1 3 - R 2 3

Como já achamos a massa m agora é só voltar pra expressão do campo!

g = G M r 3 - R 1 3 r 2 R 1 3 - R 2 3

Passo 3

Por fim, para r > R 2 :

g = G M r 2

Agora vamos fazer um gráfico dessas brincadeiras ai de cima!

Quando r < R 1 , nosso campo é nulo

Quando R 1 < r < R 2 : nosso campo é crescente com a distância r

Quando r > R 2 : Nosso campo é decrecente com a distância r

Resposta

Para r < R 1 :

g = 0

Para R 1 < r < R 2 :

g = G M r 3 - R 1 3 r 2 R 1 3 - R 2 3

Para r > R 2 :

g = G M r 2

Quando r < R 1 , nosso campo é nulo

Quando R 1 < r < R 2 : nosso campo é crescente com a distância r

Quando r > R 2 : Nosso campo é decrecente com a distância r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um pulsar, uma estrela de densidade extremamente elevada, com uma massa M igual à do Sol 1,98 × 10 30 k g , um raio R de apenas 12 km e um período de rotação de T de 0,041 s. Qual é a difere
A Fig. 13-40 mostra duas cascas esféricas concêntricas homogêneas de massas M 1 e M 2 . Determine o módulo da força gravitacional a que está sujeita uma partícula de massa m situada a uma distância (a
Uma esfera maciça homogênea tem uma massa de 1,0 × 10 4 k g e um raio de 1,0 m. Qual é o módulo da força gravitacional exercida pela esfera sobre uma partícula de massa m localizada a uma distância de
A uma profundidade igual à metade do raio da Terra, a aceleração da gravidade vale cerca de: g 2 g g 2 g 4 g 8 Não se pode determinar a resposta com os dados fornecidos.
Na superfície da Lua, a aceleração da gravidade vale a .A uma distância do centro da Lua igual a quatro vezes o raio da Lua, a aceleração da gravidade vale: 16 a a 4 a 3 a 16 Nenhuma dessas respostas.