Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 70
Uma casca esférica de paredes finas com massa m e raio r parte do repouso e rola sem deslizar para baixo da trilha indicada na Figura 10.68. O diâmetro da casca é muito pequeno, se comparado com e R, e o atrito de rolamento é desprezível.
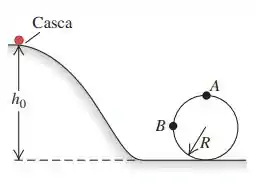
a) Qual é a altura mínima para que a casca esférica complete uma volta na parte circular da trajetória?
b) Com que intensidade a trilha empurra a casca no ponto B, que está no mesmo nível do centro da circunferência?
c) Suponha que a trilha possui atrito desprezível e que a casca foi libertada da mesma altura calculada no item (a). Nesse caso ela completaria uma volta? Como você sabe?
d) No item (c), com que intensidade a trilha empurra a casca no ponto A, o topo da circunferência? Com que intensidade ela empurrou a casca no item (a)?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma casca esférica de paredes finas com massa e raio parte do repouso e rola sem deslizar para baixo conforme a figura:
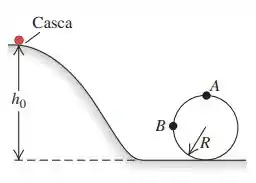
Queremos encontrar a altura mínima para que a casca esférica complete uma volta na parte circular da trajetória.
Também queremos calcular a intensidade que a trilha empurra a casca no ponto B, que está no mesmo nível do centro da circunferência.
Também queremos saber se completaria uma volta supondo que a trilha possui atrito desprezível e que a casca foi libertada da mesma altura .
Por fim, queremos saber a intensidade que a trilha empurra a casca no ponto A.
Para resolver todas essas questõezinhas, iremos utilizar o princípio da conservação de energia!! 😉
Passo 2
Aplicamos a conservação de energia para encontrar sua velocidade linear nos pontos A e B.
No ponto A, temos que, pela Segunda Lei de Newton:
Onde é força, é a massa e é a aceleração.
As forças envolvidas no ponto são a normal e a peso.
À medida que a concha rola ao longo da pista, ela tem energia cinética de translação e rotação, por isso apresenta uma aceleração que é .
Onde é a normal, é a aceleração da gravidade e é o raio.
A velocidade mínima para a casca não cair da faixa é quando a normal tende a zero, logo,
Passo 3
No ponto A, e .
Sabendo que as energias potencial e cinética iniciais são iguais as energias potencial e cinética finais, temos:
Substituindo os valores, temos:
Passo 4
Como e o momento de inércia é , então
Substituindo...
Passo 5
No ponto B, , então
Sendo ,
Sendo,
Passo 6
Supondo que a trilha possui atrito desprezível e que a casca foi libertada da mesma altura calculada no item (a). Nesse caso ela completaria uma volta? Analisamos a energia cinética
A concha estaria se movendo mais rápido em A do que com o atrito e ainda faria o loop completo.
Passo 7
Respondendo o item (d), com que intensidade a trilha empurra a casca no ponto A, o topo da circunferência? (para a letra c)
A altura seria,
Com,
No ponto A, temos
Para a letra (a), , pois neste momento a gravidade fornece a força líquida descendente que é necessário para o movimento circular.
Resposta
a)
b)
c) Analisamos a energia cinética . A concha estaria se movendo mais rápido em A do que com o atrito e ainda faria o loop completo.
d) Na letra (c) temos, ; Na letra (a), .